题目内容
如图求证:AD2=AC·AE-DF·CD.
图
证明:连结AF、DE,
∵AD为直径,∴∠AED=90°,∠AFD=90°.
∴∠CED=90°.∵∠CBD=90°,
∴B、C、E、D四点共圆.
∴AE·AC=AD·AB.
又A、F、B、C四点共圆,
∴AD·BD=DF·CD.
∴AC·AE-DF·CD=AD·AB-AD·BD=AD(AB-BD)=AD2.
∴AD2=AC·AE-DF·CD.
练习册系列答案
阅读快车系列答案
相关题目
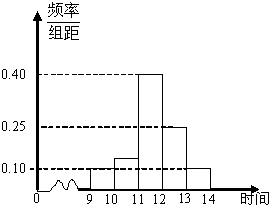某商场在国庆黄金周的促销活动中，对10月2日9时到14时的销售额进行统计，其频率分布直方图如图所示，已知9时至10时的销售额为2.5万元，则11时到12时的销售额为（ ）| A、6万元 | B、8万元 | C、10万元 | D、12万元 |
（2010•河西区二模）某商场在五一促销活动中，对5月1日9时至14时的销售额进行统计，某频率分布直方图如图所示，已知9时至10时的销售额为2.5万元，则11时至12时的销售额为（ ）
，同侧前后两轮胎之间的距离(指轮胎中心之间距离)为
(假定四个轮胎中心构成一个矩形). 当该型号汽车开上一段上坡路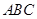
（如图(1)所示，其中
(
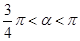)）,且前轮
已在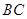
段上时，后轮中心在
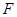位置；若前轮中心到达
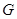处时，后轮中心在
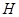处(假定该汽车能顺利驶上该上坡路). 设前轮中心在
和
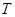，且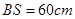
,
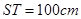. (其它因素忽略不计)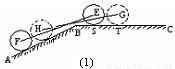
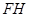和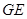
的延长线交于点
，
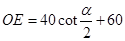(cm)；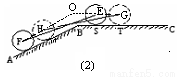
=
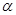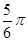时，后轮中心从