题目内容
如图,A、B分别是异面直线a、b上的两点,自AB的中点O作平面α与a、b都平行,M、N分别是a、b上的另外的两点,MN与α交于点P.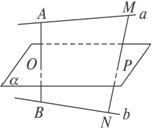
求证:P是MN的中点.
证明:连结AN交α于Q,连结OQ、PQ.
∵b∥α,OQ是过b的平面ABN与α的交线,
∴b∥OQ.
同理,PQ∥a.
在△ABN中,O是AB的中点,OQ∥BN,
∴Q是AN的中点.
又∵PQ∥AM,∴P是MN的中点.
小结:连结AN后,形成了两个平面,即平面ABN和平面AMN,为利用直线和平面平行的性质定理创造了条件,将“直线与平面平行”转化成了“直线与直线平行”.

练习册系列答案
相关题目



