题目内容
如图4,A、B分别是异面直线a、b上两点,自AB的中点O作平面α与a、b分别平行,M、N分别是a、b上的任意两点,MN与α交于点P.
图4
求证:P是MN的中点.
思路分析:连接AN交α于Q,连结OQ、PQ,
从而在△ABN和△AMN中利用中位线的性质求解.
证明:连接AN交α于Q,连结OQ、PQ,
∵b∥α,OQ是过直线b的平面ABN与α的交线,
∴b∥OQ.同理PQ∥a.
在△ABN中,O是AB的中点,OQ∥BN,
∴Q是AN的中点.
又∵PQ∥a,
∴P是MN的中点.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
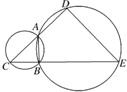
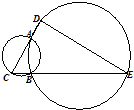（几何证明选讲选做题） 如图，A、B是两圆的交点，AC是小圆的直径，D和E分别是CA和CB的延长线与大圆的交点，已知AC=4，BE=10，且BC=AD，则DE=
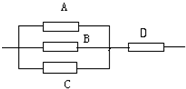如图，A，B，C，D表示4种开关，设在某段时间内它们能通电的概率是分别是0.9，0.8，0.7，0.8，那么该系统能通电的概率是
如图，A，B分别是单位圆与x轴，y轴正半轴的交点，点P为单位圆的