题目内容
如图5所示,四棱锥P—ABCD的底面ABCD是半径为R的圆的内接四边形,其中BD是圆的直径,∠ABD=60°,∠BDC=45°,△ADP∽△BAD.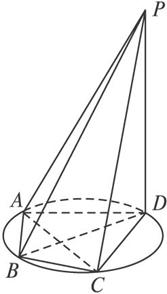
图5
(1)求线段PD的长;
(2)若PC=![]() R,求三棱锥P—ABC的体积.
R,求三棱锥P—ABC的体积.
解:(1)由BD是圆的直径,知∠BAD=90°,BD=2R.
∵∠ABD=60°,
∴AD=BDsin60°=![]() R,AB=R.
R,AB=R.
由△ADP∽△BAD,知△ADP是直角三角形,
且∠PAD=60°.
故PD=ADsin60°=3R.
(2)由BD是圆的直径,∠BDC=45°,知△BCD为直角三角形,
故DC=BDcos45°=![]() R,
R,
∵在△PDC中有PD2+CD2=9R2+2R2=11R2=PC2,
∴PD⊥CD.
由(1)知PD⊥AD,所以PD是三棱锥P—ABC在底面上的高,
∴S△ABC=![]() AB·BCsin(60°+45°)=
AB·BCsin(60°+45°)=![]() R·
R·![]() R(
R(![]() +
+![]() ×
×![]() )=
)=![]() .
.
故三棱锥P—ABC的体积为V=![]() S△ABC·PD=
S△ABC·PD=![]() ·
·![]() R2·3R=
R2·3R=![]() R3.
R3.

练习册系列答案
相关题目
 如图所示,四棱锥P-ABCD的底面ABCD是边长为a的正方形,侧棱PA=a,PB=PD=
如图所示,四棱锥P-ABCD的底面ABCD是边长为a的正方形,侧棱PA=a,PB=PD=
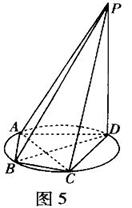

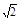 a,则它的5个面中,互相垂直的面有
对.
a,则它的5个面中,互相垂直的面有
对.