题目内容
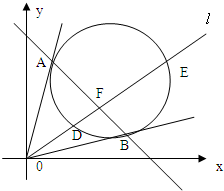 已知圆C:(x-2)2+(y-2)2=2,过原点O作圆C的切线OA、OB,切点依次记为A、B,过原点O引直线l交圆C与D、E两点,交AB与F点.
已知圆C:(x-2)2+(y-2)2=2,过原点O作圆C的切线OA、OB,切点依次记为A、B,过原点O引直线l交圆C与D、E两点,交AB与F点.
(1)求直线AB的直线方程.
(2)求OD+OE的最大值.
解:(1)由题意,O,A,C,B四点共圆,
因为圆C:(x-2)2+(y-2)2=2,圆心坐标为(2,2),半径为
所以O,A,C,B四点所在圆的圆心坐标为(1,1),圆的半径为
所以O,A,C,B四点所在圆的方程为(x-1)2+(y-1)2=2,
因为圆C:(x-2)2+(y-2)2=2,
∴两圆相减,可得公共弦,即直线AB的方程为x+y-3=0;
(2)设直线l:y=kx,代入圆C:(x-2)2+(y-2)2=2,消去y可得(1+k2)x2-(4+4k)x+6=0
设D(x1,y1),E(x2,y2),则OD+OE= (x1+x2)=4
(x1+x2)=4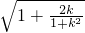 ≤4
≤4
∴OD+OE的最大值为4 .
.
分析:(1)先求得O,A,C,B四点所在圆的方程,再两圆相减,可得公共弦,即直线AB的方程;
(2)设l的方程,代入圆的方程,表示出OD+OE,即可求得结论.
点评:本题考查圆的方程,考查两圆的位置关系,考查直线与圆的位置关系,考查学生的计算能力,属于基础题.
因为圆C:(x-2)2+(y-2)2=2,圆心坐标为(2,2),半径为

所以O,A,C,B四点所在圆的圆心坐标为(1,1),圆的半径为

所以O,A,C,B四点所在圆的方程为(x-1)2+(y-1)2=2,
因为圆C:(x-2)2+(y-2)2=2,
∴两圆相减,可得公共弦,即直线AB的方程为x+y-3=0;
(2)设直线l:y=kx,代入圆C:(x-2)2+(y-2)2=2,消去y可得(1+k2)x2-(4+4k)x+6=0
设D(x1,y1),E(x2,y2),则OD+OE=
 (x1+x2)=4
(x1+x2)=4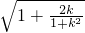 ≤4
≤4
∴OD+OE的最大值为4
 .
.分析:(1)先求得O,A,C,B四点所在圆的方程,再两圆相减,可得公共弦,即直线AB的方程;
(2)设l的方程,代入圆的方程,表示出OD+OE,即可求得结论.
点评:本题考查圆的方程,考查两圆的位置关系,考查直线与圆的位置关系,考查学生的计算能力,属于基础题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
已知圆C:(x-2)2+(y-1)2=25,过点M(-2,4)的圆C的切线l1与直线l2:ax+3y+2a=0平行,则l1与l2间的距离是( )
A、
| ||
B、
| ||
C、
| ||
D、
|