题目内容
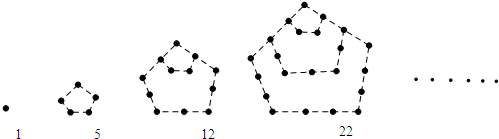
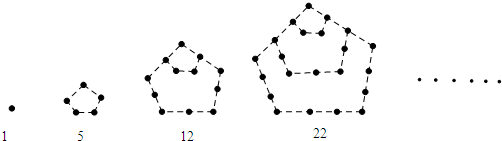
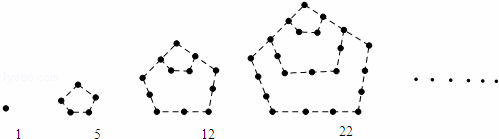
如图中的实心点个数1,5,12,22,…,被称为五角形数,其中第1个五角形数记作a1=1,第2个五角形数记作a2=5,第3个五角形数记作a3=12,第4个五角形数记作a4=22,…,若按此规律继续下去,则a5=
35
35
;若an=590,则n=20
20
.
分析:利用观察法各个图形中实心点的个数,找到个数之间的通项公式,再求第5个五角星的中实心点的个数及an=590时,n的值即可.
解答:解:第一个有1个实心点,
第二个有1+1×3+1=5个实心点,
第三个有1+1×3+1+2×3+1=12个实心点,
第四个有1+1×3+1+2×3+1+3×3+1=22个实心点,
…
第n个有1+1×3+1+2×3+1+3×3+1+…+3(n-1)+1=
+n个实心点
故当n=5时,
+n=
+5=35个实心点,
若an=590,即
+n=590,解得n=20
故答案为:35,20.
第二个有1+1×3+1=5个实心点,
第三个有1+1×3+1+2×3+1=12个实心点,
第四个有1+1×3+1+2×3+1+3×3+1=22个实心点,
…
第n个有1+1×3+1+2×3+1+3×3+1+…+3(n-1)+1=
| 3n(n-1) |
| 2 |
故当n=5时,
| 3n(n-1) |
| 2 |
| 3×4×5 |
| 2 |
若an=590,即
| 3n(n-1) |
| 2 |
故答案为:35,20.
点评:本题考查了图形的变化类问题,解题的关键是仔细观察每个图形并从中找到通项公式,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目