题目内容
20.已知,|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=2,且$\overrightarrow{OA}•\overrightarrow{OB}$=2,(1)求|$\overrightarrow{OA}+\overrightarrow{OB}$|
(2)若点C满足$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{0}$,求三角形ABC的面积.
分析 (1)根据条件即可求出$|\overrightarrow{OA}+\overrightarrow{OB}{|}^{2}$的值,从而可求出$|\overrightarrow{OA}+\overrightarrow{OB}|$的值;
(2)根据$\overrightarrow{OA}•\overrightarrow{OB}=2$即可求得∠AOB=60°,从而得出△AOB为等边三角形,可取AB中点D,从而可求出OD=$\sqrt{3}$,并且OD⊥AB.而由$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}$可得到$\overrightarrow{OC}=-2\overrightarrow{OD}$,这样即得出C,O,D三点共线,并且可求得CD=$3\sqrt{3}$,这样即可求出△ABC的面积.
解答 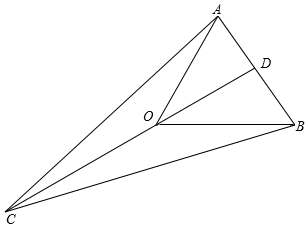 解:(1)$|\overrightarrow{OA}+\overrightarrow{OB}{|}^{2}={\overrightarrow{OA}}^{2}+2\overrightarrow{OA}•\overrightarrow{OB}+{\overrightarrow{OB}}^{2}$=4+4+4=12;
解:(1)$|\overrightarrow{OA}+\overrightarrow{OB}{|}^{2}={\overrightarrow{OA}}^{2}+2\overrightarrow{OA}•\overrightarrow{OB}+{\overrightarrow{OB}}^{2}$=4+4+4=12;
∴$|\overrightarrow{OA}+\overrightarrow{OB}|=2\sqrt{3}$;
(2)$\overrightarrow{OA}•\overrightarrow{OB}=|\overrightarrow{OA}||\overrightarrow{OB}|cos∠AOB=4cos∠AOB=2$;
∴$cos∠AOB=\frac{1}{2}$;
∴∠AOB=60°;
如图,△AOB,∠AOB=60°,OA=OB=2,取AB中点D,连接OD;
△AOB为等边三角形,∴AB=2,且OD⊥AB;
由$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}$得,$\overrightarrow{OC}=-(\overrightarrow{OA}+\overrightarrow{OB})=-2\overrightarrow{OD}$;
∴C,O,D三点共线,且$OC=2OD=2\sqrt{3}$;
∴$CD=3\sqrt{3}$;
∴${S}_{△ABC}=\frac{1}{2}×2×3\sqrt{3}=3\sqrt{3}$.
点评 考查通过求$|\overrightarrow{OA}+\overrightarrow{OB}{|}^{2}$而求$|\overrightarrow{OA}+\overrightarrow{OB}|$的方法,向量数量积的计算公式,已知三角函数值求角,等边三角形的中线也是高线,向量的数乘运算,向量数乘的几何意义,以及三角形的面积公式.

| A. | -$\frac{7}{9}$ | B. | -$\frac{1}{9}$ | C. | $\frac{1}{9}$ | D. | $\frac{7}{9}$ |
| A. | 2 | B. | -2 | C. | 6 | D. | -6 |
 执行如图所示的程序框图,若输入a=7,b=1,则输出S的值为( )
执行如图所示的程序框图,若输入a=7,b=1,则输出S的值为( )| A. | 16 | B. | 19 | C. | 34 | D. | 50 |

| A. | $\frac{19}{20}$ | B. | $\frac{20}{21}$ | C. | $\frac{21}{22}$ | D. | $\frac{22}{23}$ |
 如图所示,四边形ABCD是腰长为2的等腰梯形,其上底长为2,下底长为4,E是腰BC上一点,P为上底CD上一点,且$\overrightarrow{BE}$=$λ\overrightarrow{BC}$,$\overrightarrow{DP}$=$λ\overrightarrow{DC}$,λ∈[0,1],则$\overrightarrow{AP}$•$\overrightarrow{AE}$的取值范围是[4,10].
如图所示,四边形ABCD是腰长为2的等腰梯形,其上底长为2,下底长为4,E是腰BC上一点,P为上底CD上一点,且$\overrightarrow{BE}$=$λ\overrightarrow{BC}$,$\overrightarrow{DP}$=$λ\overrightarrow{DC}$,λ∈[0,1],则$\overrightarrow{AP}$•$\overrightarrow{AE}$的取值范围是[4,10].