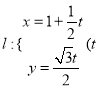题目内容
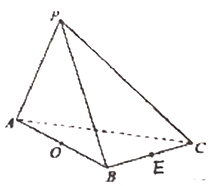
【题目】在三棱锥![]() 中,
中, ![]() 和
和![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形, ![]() ,
, ![]() 是
是![]() 中点,
中点, ![]() 是
是![]() 中点.
中点.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值的大小;
所成角的正弦值的大小;
(Ⅲ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 的余弦值为
的余弦值为![]() ?若存在,指出点
?若存在,指出点![]() 在
在![]() 上的位置;若不存在,说明理由.
上的位置;若不存在,说明理由.
【答案】(Ⅰ)见解析;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() 在棱
在棱![]() 上靠近点
上靠近点![]() 的三等分点处.
的三等分点处.
【解析】试题分析:(Ⅰ)连接![]() ,
, ![]() ,
, ![]() 中,
中, ![]() 为
为![]() 中点,易得
中点,易得![]() ,同理可得:
,同理可得: ![]() ,进而利用面面垂直的判定定理,即可证明平面
,进而利用面面垂直的判定定理,即可证明平面![]() 平面
平面![]() ;
;
(Ⅱ)以![]() 为原点,以
为原点,以![]() 方向分别为
方向分别为![]() ,
, ![]() ,
, ![]() 轴正方向建立空间直角坐标系,求得平面
轴正方向建立空间直角坐标系,求得平面![]() 的一个法向量为
的一个法向量为![]() ,利用向量的夹角公式,即可求解线面角的正弦值;
,利用向量的夹角公式,即可求解线面角的正弦值;
(Ⅲ)设![]() 得
得![]() 再求得平面
再求得平面![]() 的一个法向量为
的一个法向量为![]() 和面
和面![]() 的一个法向量为
的一个法向量为![]() ,利用向量的夹角公式,求解
,利用向量的夹角公式,求解![]() 的值,从而确定点的位置.
的值,从而确定点的位置.
试题解析:(Ⅰ)证明:连接![]() ,
, ![]() ,
, ![]() 中,
中, ![]() 为
为![]() 中点,易得
中点,易得![]() 且
且![]() .
.
同理可得: ![]() ,
, ![]() ,又∵
,又∵![]() ,∴
,∴![]() ,
,
∴![]() ,又∵
,又∵![]() ,∴
,∴![]() 平面
平面![]() ,又∵
,又∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(Ⅱ)以![]() 为原点,以
为原点,以![]() 方向分别为
方向分别为![]() ,
, ![]() ,
, ![]() 轴正方向建立空间直角坐标系,
轴正方向建立空间直角坐标系,
得![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,则有
,则有![]() ,
, ![]() ,
,
![]() ,设直线
,设直线![]() 与面
与面![]() 所成的角为
所成的角为![]() ,
,
则![]() .
.
(Ⅲ)设在棱![]() 上存在点
上存在点![]() ,设
,设![]()
![]()
设平面![]() 的一个法向量为
的一个法向量为![]()
则有![]() ,且
,且![]() ,取
,取![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
∵![]() 平面
平面![]() ,
,
∴设面![]() 的一个法向量为
的一个法向量为![]() .
.
设面![]() 与面
与面![]() 所成二面角为
所成二面角为![]() ,
,
 ,
,
解得: ![]() 或
或![]() (舍),∴
(舍),∴![]() .
.
所以存在点![]() 且当
且当![]() 在棱
在棱![]() 上靠近点
上靠近点![]() 的三等分点处,满足题意.
的三等分点处,满足题意.

【题目】某市2010年至2016年新开楼盘的平均销售价格![]() (单位:千元/平米)的统计数据如下表:
(单位:千元/平米)的统计数据如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格y | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,分析2010年至2016年该市新开楼盘平均销售价格的变化情况,并预测该市2018年新开楼盘的平均销售价格.
附:参考数据及公式: ![]() ,
, 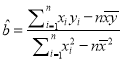 ,
, ![]() .
.