题目内容
 把函数y=sin(ωx+φ)(ω>0,|φ|<
把函数y=sin(ωx+φ)(ω>0,|φ|< )的图象按向量
)的图象按向量 平移,所得函数图象的一部分如图所示,则ω,φ的值分别是________,________.
平移,所得函数图象的一部分如图所示,则ω,φ的值分别是________,________.
2 
分析:根据所给的函数平移的向量,根据左加右减和写出平移后的解析式,得到的解析式与所给的三角函数的图象一致,根据所给的函数的图象,看出周期得到ω的值,根据图象过一个点,把点的坐标代入,根据φ的范围得到结果.
解答:由题意知将函数y=sin(ωx+φ)的图象按向量 平移,
平移,
得到函数 y=sin[ω(x+ )+φ]的图象,这个函数的图象即为所给的函数的图象,
)+φ]的图象,这个函数的图象即为所给的函数的图象,
根据三角函数的图象可以看出 =
=
∴T=π
∴ω= =
=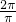 =2
=2
根据函数的图象过( )
)
∴-1=sin(2× +φ)
+φ)
∴ φ=2kπ-
φ=2kπ- ,k∈z
,k∈z
∴φ=2kπ- ,k∈z
,k∈z
∵|φ|<
∴k=1时,φ=
故答案为:2;
点评:本题考查函数图象的平移和根据三角函数的图象确定函数的解析式,本题解题的关键有两点,一是掌握向量平移的大小和方向,二是注意初相的求法,本题是一个中档题目.

分析:根据所给的函数平移的向量,根据左加右减和写出平移后的解析式,得到的解析式与所给的三角函数的图象一致,根据所给的函数的图象,看出周期得到ω的值,根据图象过一个点,把点的坐标代入,根据φ的范围得到结果.
解答:由题意知将函数y=sin(ωx+φ)的图象按向量
 平移,
平移,得到函数 y=sin[ω(x+
 )+φ]的图象,这个函数的图象即为所给的函数的图象,
)+φ]的图象,这个函数的图象即为所给的函数的图象,根据三角函数的图象可以看出
 =
=
∴T=π
∴ω=
 =
=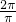 =2
=2根据函数的图象过(
 )
)∴-1=sin(2×
 +φ)
+φ)∴
 φ=2kπ-
φ=2kπ- ,k∈z
,k∈z∴φ=2kπ-
 ,k∈z
,k∈z∵|φ|<

∴k=1时,φ=

故答案为:2;

点评:本题考查函数图象的平移和根据三角函数的图象确定函数的解析式,本题解题的关键有两点,一是掌握向量平移的大小和方向,二是注意初相的求法,本题是一个中档题目.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
把函数y=sin(x+
)图象上各点的横坐标缩短到原来的
倍(纵坐标不变),再将图象向右平移
个单位,那么所得图象的一条对称轴方程为( )
| π |
| 6 |
| 1 |
| 2 |
| π |
| 3 |
A、x=-
| ||
B、x=-
| ||
C、x=
| ||
D、x=
|