题目内容
如图,PA垂直于矩形ABCD所在的平面,AD=PA=2, ,E,F分别是AB、PD的中点.
,E,F分别是AB、PD的中点.
(Ⅰ)求证:AF∥平面PCE;
(Ⅱ)求证:平面PCE⊥平面PCD;
(Ⅲ)求二面角F﹣EC﹣D的大小.
 ,E,F分别是AB、PD的中点.
,E,F分别是AB、PD的中点.(Ⅰ)求证:AF∥平面PCE;
(Ⅱ)求证:平面PCE⊥平面PCD;
(Ⅲ)求二面角F﹣EC﹣D的大小.

解:(Ⅰ)证明:设G为PC的中点,连接FG,EG,
∵F为PD的中点,E为AB的中点,
∴FG
 CD,AE
CD,AE
 CD
CD
∴FG AE,
AE,
∴AF∥GE
∵GE 平面PEC,
平面PEC,
∴AF∥平面PCE;
(Ⅱ)证明:∵PA=AD=2,
∴AF⊥PD
又∵PA⊥平面ABCD,CD 平面ABCD,
平面ABCD,
∴PA⊥CD,
∵AD⊥CD,PA∩AD=A,
∴CD⊥平面PAD,
∵AF 平面PAD,
平面PAD,
∴AF⊥CD.
∵PD∩CD=D,
∴AF⊥平面PCD,
∴GE⊥平面PCD,
∵GE 平面PEC,
平面PEC,
∴平面PCE⊥平面PCD;
(Ⅲ)取AD的中点M,连接FM,EM,MC,
∵F是PD的中点;
∴FM∥PA;
∴FM⊥平面ABCD;?EC⊥FM①
在三角形EMC中,
∵MC= =3;ME=
=3;ME= =
= ;EC=
;EC= =
= ;
;
∴MC2=ME2+EC2;
∴EM⊥EC ②;
∴由①②得EC⊥平面FME,
∴EC⊥FE,即∠FEM为二面角F﹣EC﹣D的平面角,
而tan∠FEM= =
= =
= =
= ;
;
∴∠FEM=30°.故二面角F﹣EC﹣D为30°.



练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 如图,PA垂直于矩形ABCD所在的平面,AD=PA=2,CD=2
如图,PA垂直于矩形ABCD所在的平面,AD=PA=2,CD=2 如图,PA垂直于矩形ABCD所在的平面,E、F分别是AB、PD的中点.
如图,PA垂直于矩形ABCD所在的平面,E、F分别是AB、PD的中点. 如图,PA垂直于矩形ABCD所在的平面,M、N分别是AB、PC的中点
如图,PA垂直于矩形ABCD所在的平面,M、N分别是AB、PC的中点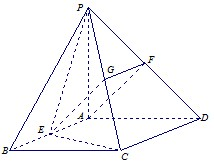 如图,PA垂直于矩形ABCD所在平面,PA=AD,E、F分别是AB、PD的中点.
如图,PA垂直于矩形ABCD所在平面,PA=AD,E、F分别是AB、PD的中点. 如图,PA垂直于矩形ABCD所在的平面,AD=PA=2,
如图,PA垂直于矩形ABCD所在的平面,AD=PA=2,