题目内容
20.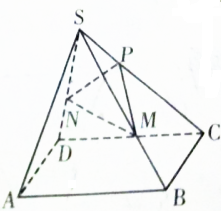 如图,四边形ABCD是正方形,S为四边形ABCD所在平面外一点,SA=SB=SC=SD,P,M,N分别是SC,SB,SD上的点,且PC:SP=SM:MB=SN:ND=2:1,求证:SA∥平面PMN.
如图,四边形ABCD是正方形,S为四边形ABCD所在平面外一点,SA=SB=SC=SD,P,M,N分别是SC,SB,SD上的点,且PC:SP=SM:MB=SN:ND=2:1,求证:SA∥平面PMN.
分析 连结AC、BD,交于点G,取SC的中点H,连接BH、DH、GH,由已知条件推导出面HBD‖面PMN,再由中位线定理得到SA‖GH,由此能证明SA‖面PMN.
解答 证明:连结AC、BD,交于点G,取SC的中点H,连接BH、DH、GH,
∵四边形ABCD是正方形,S为四边形ABCD所在平面外一点,
SA=SB=SC=SD,P,M,N分别是SC,SB,SD上的点,且PC:SP=SM:MB=SN:ND=2:1,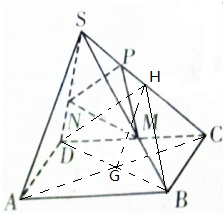
∴$\frac{SP}{PH}=\frac{SM}{MB}=\frac{SN}{ND}=2$,
∴PM∥HB,PN∥HD,
∵PM∩PN=P,HB∩HD=H,
PM?平面PMN,PN?平面PMN,HB?平面HBD,HD?平面HBD,
∴面HBD‖面PMN
又GH?面HBD,所以GH‖面PMN
在△SAC中,G、H分别是AC、SC中点,∴SA‖GH,
综上所述,SA‖GH,GH‖面PMN,
∴SA‖面PMN.
点评 本题考查线面垂直的证明,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
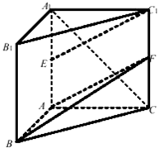 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=$\frac{\sqrt{2}}{2}A{A}_{1}$,E是棱A1A的中点,F为棱CC1上的一动点.
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=$\frac{\sqrt{2}}{2}A{A}_{1}$,E是棱A1A的中点,F为棱CC1上的一动点.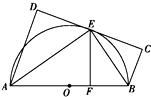 如图,AB为☉O的直径,直线CD与☉O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,连接AE,BE.求证:∠FEB=∠CEB.
如图,AB为☉O的直径,直线CD与☉O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,连接AE,BE.求证:∠FEB=∠CEB.