Question

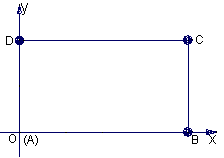
在平面直角坐标系中，已知矩形ABCD的长为2，宽为1，AB、AD边分别在x轴、y轴的正半轴上，A点与坐标原点重合（如下图所示）。将矩形折叠，使A点落在线段DC上，
（Ⅰ）若折痕所在直线的斜率为k，试写出折痕所在直线的方程；
（Ⅱ）求折痕的长的最大值。

Answer 1

解：（Ⅰ）（1）当k=0时，此时A点与D点重合，折痕所在的直线方程；
（2）当k≠0时，将矩形折叠后A点落在线段CD上的点为G（a，1），
所以A与G关于折痕所在的直线对称，有，
故G点坐标为G（-k，1），
从而折痕所在的直线与OG的交点坐标（线段OG的中点）为，
折痕所在的直线方程；
由（1）（2）得折痕所在的直线方程为：k=0时，；
k≠0时，；
（Ⅱ）（1）当k≠0时，折痕的长为2；
（2）当k≠0时，折痕所在的直线与坐标轴的交点坐标为，
，
，
令y′=0解得，
∴；
所以折痕的长度的最大值2。