Question

已知a、b∈（0，+∞），且a+b=1,求证：

(1)a²+b²≥;

(2)+≥8;

(3)+ ≥;

(4) ≥.

Answer 1

证明见解析

解析:

由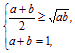 a、b∈（0，+∞），

得≤ab≤≥4.

（当且仅当a=b=时取等号）

(1)∵a²+b²=(a+b)²-2ab=1-2ab≥1-2×=，

∴a²+b²≥.

(2)∵+≥≥8,∴+≥8.

(3)由(1)、(2)的结论，知

+ =a²+b²+4++

≥+4+8=,∴+ ≥.

 (4) =++ab+

=+++2≥2++2=.