题目内容
在四面体S-ABC中,AB⊥BC,AB=BC=
,SA=SC=2,二面角S-AC-B的余弦值是-
,则该四面体外接球的表面积是( )
| 2 |
| ||
| 3 |
A、8
| ||
B、
| ||
| C、6π | ||
D、
|
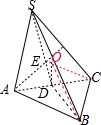
分析:取AC中点D,连接SD,BD,由题意可得∠SDB为二面角S-AC-B,取等边△SAC的中心E,找出O点为四面体的外接球球心.
解答:解:取AC中点D,连接SD,BD,
因为AB=BC=
,所以BD⊥AC,
因为SA=SC=2,所以SD⊥AC,AC⊥平面SDB.
所以∠SDB为二面角S-AC-B.
在△ABC中AB⊥BC,AB=BC=
,
所以AC=2.
取等边△SAC的中心E,作EO⊥平面SAC,
过D作DO⊥平面ABC,O为外接球球心,
所以ED=
,二面角S-AC-B的余弦值是-
,所以cos∠EDO=
,OD=
,
所以BO=
=
=OA=OS=OC
所以O点为四面体的外接球球心,
其半径为
,表面积为6π.
故选C.
因为AB=BC=
| 2 |
因为SA=SC=2,所以SD⊥AC,AC⊥平面SDB.
所以∠SDB为二面角S-AC-B.
在△ABC中AB⊥BC,AB=BC=
| 2 |
所以AC=2.
取等边△SAC的中心E,作EO⊥平面SAC,
过D作DO⊥平面ABC,O为外接球球心,
所以ED=
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 2 |
所以BO=
| BD2+OD2 |
| ||
| 2 |
所以O点为四面体的外接球球心,

其半径为
| ||
| 2 |
故选C.
点评:解决此类问题的关键是熟悉几何体的结构特征,利用已知条件求出线段长度,进而确定圆心的位置即可求出圆的半径,

练习册系列答案
相关题目
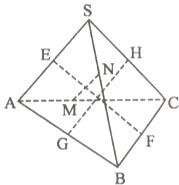 如图,在四面体S-ABC中,E、F、G、H、M、N分别是棱SA、BC、AB、SC、AC、SB的中点,且EF=GH=MN,求证:SA⊥BC,SB⊥AC,SC⊥AB.
如图,在四面体S-ABC中,E、F、G、H、M、N分别是棱SA、BC、AB、SC、AC、SB的中点,且EF=GH=MN,求证:SA⊥BC,SB⊥AC,SC⊥AB.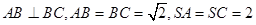 ,二面角S—AC—B的余弦值是
,二面角S—AC—B的余弦值是 ,则该四面体外接球的表面积是 ( )
,则该四面体外接球的表面积是 ( )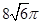 B.
B.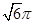 C.24
C.24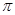 D.6
D.6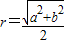 ,将此结论拓展到空间,可得出的正确结论是:在四面体S-ABC中,若SA、SB、SC两两垂直,SA=a,SB=b,SC=c,则四面体S-ABC的外接球半径R= .
,将此结论拓展到空间,可得出的正确结论是:在四面体S-ABC中,若SA、SB、SC两两垂直,SA=a,SB=b,SC=c,则四面体S-ABC的外接球半径R= .