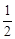题目内容
已知双曲线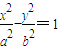 的焦点到渐近线的距离为
的焦点到渐近线的距离为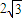 ,且双曲线右支上一点P到右焦点的距离的最小值为2,则双曲线的离心率为( )
,且双曲线右支上一点P到右焦点的距离的最小值为2,则双曲线的离心率为( )A.
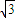
B.3
C.2
D.

【答案】分析:根据双曲线性质可知双曲线右支上一点P到右焦点的距离的最小时,p在右顶点上,进而求得c-a的值,然后利用点到直线的距离表示出焦点到渐近线的距离,求得a和c的关系式,最后两关系式联立求得a和c,则离心率可得.
解答:解:依题意可知双曲线右支上一点P到右焦点的距离的最小时,P在右顶点上,即c-a=2①
∵焦点到渐近线的距离为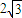 ,
,
即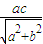 =2
=2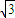 ,②
,②
①②联立求得a=2,c=4
∴e=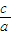 =2
=2
故选C.
点评:本题主要考查了双曲线的简单性质.考查了学生数形结合的思想,解析几何知识的综合运用.
解答:解:依题意可知双曲线右支上一点P到右焦点的距离的最小时,P在右顶点上,即c-a=2①
∵焦点到渐近线的距离为
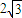 ,
,即
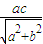 =2
=2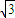 ,②
,②①②联立求得a=2,c=4
∴e=
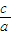 =2
=2故选C.
点评:本题主要考查了双曲线的简单性质.考查了学生数形结合的思想,解析几何知识的综合运用.

练习册系列答案
相关题目
已知双曲线的焦点到渐近线的距离等于右焦点到右顶点的距离的2倍,则双曲线的离心率e的值为( )
A、
| ||
B、
| ||
C、
| ||
| D、2 |
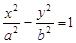 的焦点到渐近线的距离为
的焦点到渐近线的距离为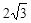 ,且双曲线右支上一点
,且双曲线右支上一点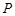 到右焦点的距离的最小值为2,则双曲线的离心率为( )
到右焦点的距离的最小值为2,则双曲线的离心率为( ) B、3 C、2 D、
B、3 C、2 D、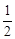
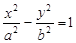 的焦点到渐近线的距离为
的焦点到渐近线的距离为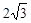 ,且双曲线右支上一点
,且双曲线右支上一点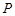 到右焦点的距离的最小值为2,则双曲线的离心率为( )
到右焦点的距离的最小值为2,则双曲线的离心率为( )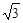 (B)3
(C)2
(D)
(B)3
(C)2
(D)