题目内容
(2012•道里区三模)已知数列{an}的前n项和为Sn,满足Sn=n2an-n2(n-1),且a1=
.
(1)令bn=
Sn,确定bn与bn-1(n≥2)的关系;
(2)求{an}的通项.
| 1 |
| 2 |
(1)令bn=
| n+1 |
| n |
(2)求{an}的通项.
分析:(1)由Sn=n2an-n2(n-1),且a1=
,用迭代法能求出(n2-1)Sn=n2Sn-1+n2(n-1),再由bn=
Sn,能确定bn与bn-1(n≥2)的关系.
(2)由(1)知bn-b1=n+(n-1)+…+2=
-1,故bn=
,由此求出Sn,从而能求出{an}的通项公式.
| 1 |
| 2 |
| n+1 |
| n |
(2)由(1)知bn-b1=n+(n-1)+…+2=
| n(n+1) |
| 2 |
| n(n+1) |
| 2 |
解答:解:(1)∵Sn=n2an-n2(n-1),且a1=
,
∴当n≥2时,有an=Sn-Sn-1,
∴Sn=n2(Sn-Sn-1)-n2(n-1),
即(n2-1)Sn=n2Sn-1+n2(n-1),
∵bn=
Sn,∴Sn=
bn,
从而bn-bn-1=n.
(2)由(1)知
bn-b1=n+(n-1)+…+2=
-1,
b1=2S1=1,
∴bn=
,
∴Sn=
•bn=
•
=
,
∴a1=S1=
,
an=Sn-Sn-1=
-
=
,
当n=1时,
=
,
故an=
.
| 1 |
| 2 |
∴当n≥2时,有an=Sn-Sn-1,
∴Sn=n2(Sn-Sn-1)-n2(n-1),
即(n2-1)Sn=n2Sn-1+n2(n-1),
∵bn=
| n+1 |
| n |
| n |
| n+1 |
从而bn-bn-1=n.
(2)由(1)知
bn-b1=n+(n-1)+…+2=
| n(n+1) |
| 2 |
b1=2S1=1,
∴bn=
| n(n+1) |
| 2 |
∴Sn=
| n |
| n+1 |
| n |
| n+1 |
| n(n+1) |
| 2 |
| n2 |
| 2 |
∴a1=S1=
| 1 |
| 2 |
an=Sn-Sn-1=
| n2 |
| 2 |
| (n-1)2 |
| 2 |
| 2n-1 |
| 2 |
当n=1时,
| 2n-1 |
| 2 |
| 1 |
| 2 |
故an=
| 2n-1 |
| 2 |
点评:本题考查数列的递推公式的应用,解题时要认真审题,仔细解答,注意迭代法和等价转化思想的灵活运用.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
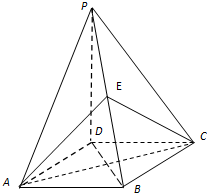 (2012•道里区三模)如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
(2012•道里区三模)如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上. (2012•道里区三模)如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数y=
(2012•道里区三模)如图,设D是图中边长分别为1和2的矩形区域,E是D内位于函数y=