题目内容
10.已知正实数a、b、c满足3a=4b=6c.求证:2bc+ac=2ab.分析 设3a=4b=6c=k,k>0,则$\frac{1}{a}$=logk3,$\frac{1}{b}=lo{g}_{k}4$,$\frac{1}{c}=lo{g}_{k}6$,由此能证明2bc+ac=2ab.
解答 证明:∵正实数a、b、c满足3a=4b=6c,
∴设3a=4b=6c=k,k>0,
则a=log3k,b=log4k,c=log6k,
∴$\frac{1}{a}$=logk3,$\frac{1}{b}=lo{g}_{k}4$,$\frac{1}{c}=lo{g}_{k}6$,
∴$\frac{2}{a}+\frac{1}{b}=lo{g}_{k}9+lo{g}_{k}4=lo{g}_{k}36=\frac{2}{c}$,
∴2bc+ac=2ab.
点评 本题考查对数式的证明,是中档题,解题时要注意对数的性质和运算法则及换底公式的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.函数y=ln(2x+5)的导函数f′(x)=( )
| A. | $\frac{1}{2x+5}$ | B. | $\frac{2}{2x+5}$ | C. | $\frac{5}{2x+5}$ | D. | $\frac{ln2}{2x+5}$ |
9.若一个命题的结论是“直线l在平面α内”,则用反证法证明这个命题时,第一步应作的假设为( )
| A. | 假设直线l∥平面α | B. | 假设直线l∩平面α于点A | ||
| C. | 假设直线l?平面α | D. | 假设直线l⊥平面α |
10.执行如图所示的程序框图,若输出的值为-105,则输入的n的值可能是( )
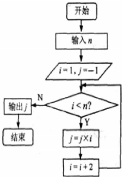

| A. | 5 | B. | 7 | C. | 8 | D. | 10 |