题目内容
(本题12分)
设函数 ,曲线
,曲线 在点M
在点M 处的切线方程为
处的切线方程为 .
.
(1)求 的解析式; (2)求函数
的解析式; (2)求函数 的单调递减区间;
的单调递减区间;
(3)证明:曲线 上任一点处的切线与直线
上任一点处的切线与直线 和直线
和直线 所围成的三角形面积为定值,并求此定值.
所围成的三角形面积为定值,并求此定值.
【答案】
(1) 的解析式的解析式为:
的解析式的解析式为:
(2) 的单调减区间为
的单调减区间为
(3)点 处的切线与直线
处的切线与直线 ,
, 所围成的三角形面积为
所围成的三角形面积为
 .
.
【解析】解:(Ⅰ)∵切点在切线上∴将点M代入切线方程解得 ………1分
………1分
由 ,………2分
,………2分
根据题意得关于a,b的方程组:
 解得:a=1,b=1………3分
解得:a=1,b=1………3分
所以 的解析式的解析式为:
的解析式的解析式为: ………4分
………4分
(Ⅱ)由 (
( )
……5分
)
……5分
令 ,解得:
,解得: ………7分
………7分
所以 的单调减区间为
的单调减区间为 ……8分
……8分
(Ⅲ)(Ⅱ)设 为曲线上任一点,由
为曲线上任一点,由 知曲线在点
知曲线在点 处的切线方程为
处的切线方程为
 ,
,
即 .
.
令 得
得 ,从而得切线与直线
,从而得切线与直线 的交点坐标为
的交点坐标为 .
.
令 得
得 ,从而得切线与直线
,从而得切线与直线 的交点坐标为
的交点坐标为 .···· 10分
.···· 10分
所以点 处的切线与直线
处的切线与直线 ,
, 所围成的三角形面积为
所围成的三角形面积为
 .
.

练习册系列答案
相关题目
 在
在 内有极值。
内有极值。 的取值范围;
的取值范围; 分别为
分别为 的极大值和极小值,记
的极大值和极小值,记 ,求S的取值范围。
,求S的取值范围。 为自然对数的底数)
为自然对数的底数)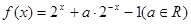 ,
,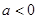 ,用单调性定义证明上是增函数。
,用单调性定义证明上是增函数。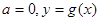 的图象与
的图象与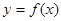 的图象关于
的图象关于 对称,求函数
对称,求函数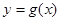 的解析式。
的解析式。 ,曲线
,曲线 在点M
在点M 处的切线方程为
处的切线方程为 .
. 的解析式; (2)求函数
的解析式; (2)求函数 和直线
和直线 所围成的三角形面积为定值,并求此定值.
所围成的三角形面积为定值,并求此定值.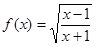 的定义域为A, 函数
的定义域为A, 函数 (其中
(其中 )的定义域为B.
)的定义域为B.  ,当a=0时,求
,当a=0时,求 ;
; , 求实数
, 求实数 的取值范围.
的取值范围.