Question

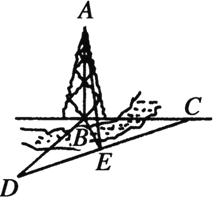
【题目】如图，某人在塔的正东方向上的处在与塔垂直的水平面内沿南偏西的方向以每小时千米的速度步行了分钟以后，在点处望见塔的底端在东北方向上，已知沿途塔的仰角，的最大值为．

（1）求该人沿南偏西的方向走到仰角最大时，走了几分钟；

（2）求塔的高．

Answer 1

【答案】（1）；（2）

【解析】

试题（1）首先在中利用正弦定理求解得到边长，进而在直角中求解得到边的长度，进而求得步行的时间；（2）由（１）知当取得最大值时解直角三角形可求得塔的高

试题解析：（1）依题意知在△中,

（ｍ）,，

由正弦定理得

∴＝（）

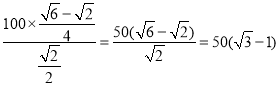在△中，

∵为定长 ∴当的长最小时，取最大值，这时

当时，在△中

（）,

设该人沿南偏西的方向走到仰角最大时，走了分钟，

则（）

（2）由（1）知当取得最大值时，，在△中,

∴＝（）

即所求塔高为米．