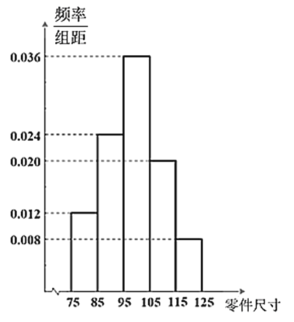
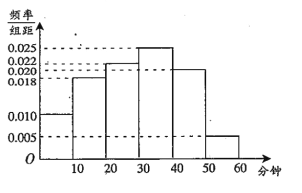
题目内容
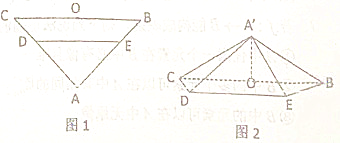
【题目】某公园内有一块以
为圆心半径为
米的圆形区域.为丰富市民的业余文化生活，现提出如下设计方案：如图，在圆形区域内搭建露天舞台，舞台为扇形
区域，其中两个端点
，
分别在圆周上；观众席为梯形
内切在圆外的区域，其中
，
，且
，
在点的同侧.为保证视听效果，要求观众席内每一个观众到舞台处的距离都不超过
米.设
，
.问：对于任意
，上述设计方案是否均能符合要求？
【答案】能符合要求
【解析】
过
作
垂直于
，垂足为
,所以点
处观众离点处最远. 由余弦定理可得
.再求得
. 因为
，所以观众席内每一个观众到舞台处的距离都不超过
米.
解：过作垂直于，垂足为.在直角三角形
中，
，
，
所以
，因此
.由图可知，点处观众离点处最远.
在三角形
中，由余弦定理可知
.
因为
，所以当
时，即
时，
，即.
因为，所以观众席内每一个观众到舞台处的距离都不超过米.
答：对于任意
，上述设计方案均能符合要求.
练习册系列答案
相关题目
