题目内容
(本小题满分12分)己知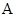 、
、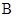 、
、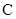 是椭圆
是椭圆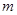 :
: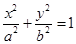 (
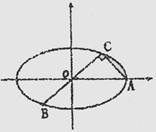
(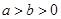 )上的三点,其中点
)上的三点,其中点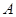 的坐标为
的坐标为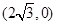 ,
,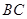 过椭圆的中心,且
过椭圆的中心,且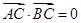 ,
, 。
。
(Ⅰ)求椭圆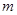 的方程;
的方程;
(Ⅱ)过点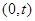 的直线
的直线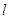 (斜率存在时)与椭圆
(斜率存在时)与椭圆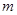 交于两点
交于两点 ,
,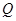 ,设
,设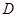 为椭圆
为椭圆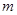 与
与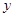 轴负半轴的交点,且
轴负半轴的交点,且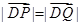 ,求实数
,求实数 的取值范围.
的取值范围.
(1) 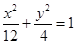 (2)
(2) 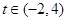
解析试题分析:.解:(Ⅰ)∵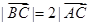 且
且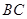 过
过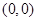 ,则
,则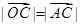 .
.
∵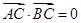 ,∴
,∴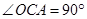 ,即
,即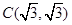 .……2分
.……2分
又∵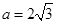 ,设椭圆
,设椭圆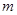 的方程为
的方程为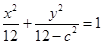 ,
,
将C点坐标代入得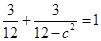 ,
,
解得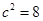 ,
,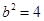 .
.
∴椭圆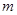 的方程为
的方程为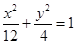 . ……5分
. ……5分
(Ⅱ)由条件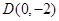 ,
,
当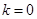 时,显然
时,显然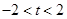 ;………6分
;………6分
当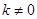 时,设
时,设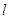 :
: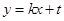 ,
, ,消
,消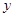 得
得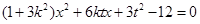
由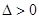 可得,
可得,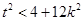 ……①………8分
……①………8分
设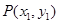 ,
,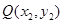 ,
,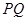 中点
中点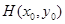 ,则
,则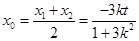 ,
,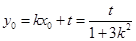 , ∴
, ∴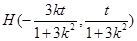 .………10分
.………10分
由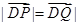 ,∴
,∴ ,即
,即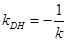 。∴
。∴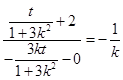 ,
,
化简得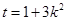 ……② ∴
……② ∴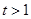 将①代入②得,
将①代入②得,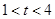 。∴
。∴ 的范围是
的范围是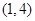 。
。
综上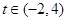 .………12
.………12
考点:直线与椭圆的位置关系
点评:解决该试题的关键是利用性质得到a,b,c的关系式,进而结合韦达定理和垂问题得到参数的方程,然后得到范围。属于基础题。

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 ,在抛物线上任意画一个点
,在抛物线上任意画一个点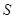 ,度量点
,度量点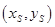 ,如图.
,如图.
 时,
时,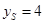 ,试求抛物线
,试求抛物线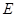 的方程;
的方程;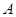 ,焦点为
,焦点为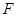 ,构造直线
,构造直线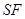 交抛物线
交抛物线 ,构造直线
,构造直线 、
、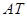 分别交准线于
分别交准线于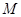 、
、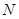 两点,构造直线
两点,构造直线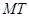 、
、 .经观察得:沿着抛物线
.经观察得:沿着抛物线 .请你证明这一结论.
.请你证明这一结论. 
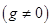 ”,其余条件不变,发现“
”,其余条件不变,发现“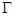 的方程为
的方程为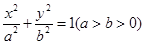 ,点P的坐标为(-a,b).
,点P的坐标为(-a,b). ,求点
,求点 的坐标;
的坐标;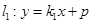 交椭圆
交椭圆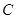 、
、 两点,交直线
两点,交直线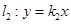 于点
于点 .若
.若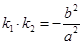 ,证明:
,证明: 的中点;
的中点;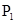 、
、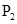 满足
满足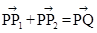 ,写出求作点
,写出求作点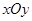 中,以O为极点,
中,以O为极点,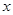 轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为
轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为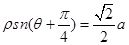 ,曲线
,曲线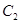 的参数方程为
的参数方程为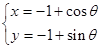 ,(
,(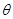 为参数,
为参数,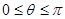 )。
)。 的取值范围。
的取值范围。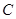 :
: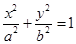 (
(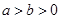 )的离心率为
)的离心率为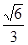 ,过右焦点
,过右焦点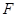 且斜率为1的直线交椭圆
且斜率为1的直线交椭圆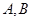 两点,
两点,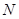 为弦
为弦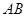 的中点。
的中点。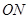 (
( 为坐标原点)的斜率
为坐标原点)的斜率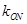 ;
;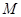 椭圆
椭圆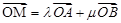 ,求
,求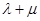 的最大值和最小值.
的最大值和最小值. 为抛物线
为抛物线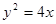 的焦点,
的焦点,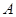 为抛物线上任意一点,已
为抛物线上任意一点,已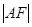 为半径画圆,与
为半径画圆,与 轴负半轴交于
轴负半轴交于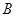 点,试判断过
点,试判断过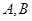 的直线与抛物线的位置关系,并证明。
的直线与抛物线的位置关系,并证明。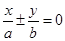 称为椭圆
称为椭圆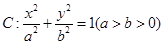 的“特征直线”,若椭圆的离心率
的“特征直线”,若椭圆的离心率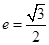 .(1)求椭圆的“特征直线”方程;
.(1)求椭圆的“特征直线”方程;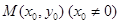 作圆
作圆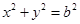 的切线,切点为P、Q,直线PQ与椭圆的“特征直线”相交于点E、F,O为坐标原点,若
的切线,切点为P、Q,直线PQ与椭圆的“特征直线”相交于点E、F,O为坐标原点,若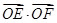 取值范围恰为
取值范围恰为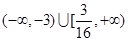 ,求椭圆C的方程.
,求椭圆C的方程. 中,已知三点
中,已知三点 ,
,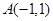 ,
, ,曲线C上任意—点
,曲线C上任意—点 满足:
满足: .
. ,
, .试探究
.试探究 的值是否与点P及直线L有关,并证明你的结论;
的值是否与点P及直线L有关,并证明你的结论; 取得最小值,求实数m的取值范围.
取得最小值,求实数m的取值范围.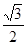 。
。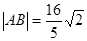 ,求直线l的方程。
,求直线l的方程。