题目内容
袋中有若干个小球，分别为红球、黑球、黄球、白球，从中任取一球，得到红球的概率是| 1 |
| 3 |
| 5 |
| 12 |
| 5 |
| 12 |
分析：设从袋中取到黑球、黄球、白球的概率依次为P（A）、P（B）、P（C），根据题意，从中任取一球，得到红球的概率是
，则P（A）+P（B）+P（C）=1-
；得到黑球或黄球的概率是
，有有P（A）+P（B）=
，得到黑球或黄球的概率是
，有P（B）+P（C）=
，解可得P（C）的值，即可得答案．
| 1 |
| 3 |
| 1 |
| 3 |
| 5 |
| 12 |
| 5 |
| 12 |
| 5 |
| 12 |
| 5 |
| 12 |
解答：解：设从袋中取到黑球、黄球、白球的概率依次为P（A）、P（B）、P（C），
根据题意，有P（A）+P（B）=
，P（B）+P（C）=
，P（A）+P（B）+P（C）=1-
，
解可得，P（B）=
，P（C）=
，
故答案为：
．
根据题意，有P（A）+P（B）=
| 5 |
| 12 |
| 5 |
| 12 |
| 1 |
| 3 |
解可得，P（B）=
| 1 |
| 6 |
| 1 |
| 4 |
故答案为：
| 1 |
| 4 |
点评：本题考查互斥事件的概率加法公式，首先注意分析题意，认清事件之间的关系，进而结合题意，建立方程组进行解答．
练习册系列答案
相关题目
：
；
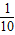