题目内容
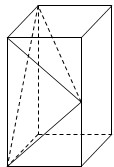 长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.
长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.(1)求证:直线AE⊥平面A1D1E;
(2)求三棱锥A-A1D1E的体积;
(3)求异面直线A1E与AD1所成角的大小.
分析:(1)根据已知中长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点,结合长方体的几何特征,我们可得AE⊥A1E,AE⊥A1D1,结合线面垂直的判定定理即可得到AE⊥平面A1D1E;
(2)由(1)的结论,我们可得AE即为三棱锥A-A1D1E的高,根据已知求出三棱锥的底面积,代入棱锥体积公式,即可求出三棱锥A-A1D1E的体积;
(3)取CC1的中点F,连接D1F,则可得∠AD1F即为求异面直线A1E与AD1所成角,在△AD1F中,可求得结论.
(2)由(1)的结论,我们可得AE即为三棱锥A-A1D1E的高,根据已知求出三棱锥的底面积,代入棱锥体积公式,即可求出三棱锥A-A1D1E的体积;
(3)取CC1的中点F,连接D1F,则可得∠AD1F即为求异面直线A1E与AD1所成角,在△AD1F中,可求得结论.
解答:(1)证明:∵长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点
∴AE=A1E=
,AA1=2,
∴AA12=AE2+A1E2
∴AE⊥A1E
又∵D1A1⊥平面A1EA,AE?平面A1EA
∴AE⊥A1D1,又D1A1∩A1E=A1,
∴AE⊥平面A1D1E;
(2)解:由(1)中AE⊥平面A1D1E,
∴VA-A1D1E=
•S△A1D1E•AE=
×
×1×
×
=
(3)解:取CC1的中点F,连接D1F,
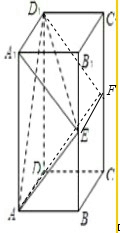
则A1E∥D1F,所以∠AD1F即为求异面直线A1E与AD1所成角.
∵AB=BC=1,AA1=2,∴D1F=
,AF=
,AD1=
∵D1F2+AF2=AD12
∴D1F⊥AF
在△AD1F中,可求得tan∠AD1F=
=
∴∠AD1F=arctan
.
∴AE=A1E=
| 2 |
∴AA12=AE2+A1E2
∴AE⊥A1E
又∵D1A1⊥平面A1EA,AE?平面A1EA
∴AE⊥A1D1,又D1A1∩A1E=A1,
∴AE⊥平面A1D1E;
(2)解:由(1)中AE⊥平面A1D1E,
∴VA-A1D1E=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 3 |
(3)解:取CC1的中点F,连接D1F,

则A1E∥D1F,所以∠AD1F即为求异面直线A1E与AD1所成角.
∵AB=BC=1,AA1=2,∴D1F=
| 2 |
| 3 |
| 5 |
∵D1F2+AF2=AD12
∴D1F⊥AF
在△AD1F中,可求得tan∠AD1F=
| ||
|
| ||
| 2 |
∴∠AD1F=arctan
| ||
| 2 |
点评:本题主要考查空间角,体积的计算,线面垂直,考查了空间想象能力、计算能力,属于中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
长方体ABCD-A1B1C1D1中,AB=3,BC=4,AA1=5 则三棱锥A1-ABC的体积为( )
| A、10 | B、20 | C、30 | D、35 |
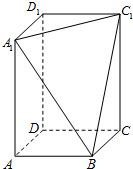 在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.
在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.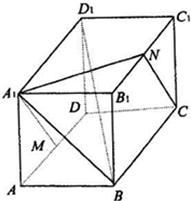 如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC=
如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC= 如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点.
如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点. 在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.
在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.