题目内容

已知P（3，m）为y²=4x上一点，则P到抛物线的焦点F的距离为

A.
2
B.
3
C.
4
D.
$数学公式$

C
分析：确定抛物线的准线方程，根据抛物线的定义，可得P到抛物线的焦点F的距离等于P到抛物线的准线的距离，由此可得结论．
解答：y²=4x的准线方程为x=-1
根据抛物线的定义，可得P到抛物线的焦点F的距离等于P到抛物线的准线的距离
∵P（3，m）
∴P到抛物线的准线的距离为3+1=4
∴P到抛物线的焦点F的距离为4
故选C．
点评：本题考查抛物线的定义，考查学生分析解决问题的能力，属于基础题．

练习册系列答案

小学奥数抢先起跑系列答案

孟建平错题本系列答案

练习精编系列答案

计算专项训练系列答案

走向优等生系列答案

一品快乐作业本系列答案

小学生应用题训练营系列答案

超能学典应用题题卡系列答案

同步阅读人民教育出版社系列答案

长江全能学案英语阅读训练系列答案

相关题目

已知P为半圆C：

（θ为参数，0≤θ≤π）上的点，点A的坐标为（1，0），O为坐标原点，点M在射线OP上，线段OM与C的弧

的长度均为

．
（1）以O为极点，x轴的正半轴为极轴建立极坐标系，求点M的极坐标；
（2）求直线AM的参数方程．

（2013•宁德模拟）已知P是函数y=f（x）（x∈[m，n]）图象上的任意一点，M、N为该图象的两个端点，点Q满足

•i=0（其中0＜λ＜1，

为x轴上的单位向量），若|

|≤T（T为常数）在区间[m，n]上恒成立，则称y=f（x）在区间[m，n]上具有“T级线性逼近”．现有函数：①y=2x+1；②y=

；③y=x²．则在区间[1，2]上具有“

级线性逼近”的函数的个数为（　　）

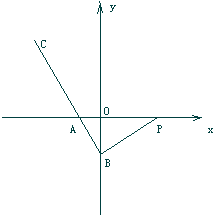如图，已知直角三角形PAB的直角顶点为B，点P的坐标为（3，0），点B在y轴上，点A在x轴的负半轴上，在BA的延长线上取一点C，使

．
（1）当B在y轴上移动时，求动点C的轨迹方程；
（2）若直线l：y=k（x-1）与点C的轨迹交于M、N两点，设D（-1，0），当∠MDN为锐角时，求的取值范围．

已知A（3，0）及双曲线E：

=1，若双曲线E的右支上的点Q到点B（m，0）（m≥3）距离的最小值为|AB|．
（1）求m的取值范围，并指出当m变化时B的轨迹C
（2）如（图1），轨迹C上是否存在一点D，它在直线y=

x上的射影为P，使得

？若存在试指出双曲线E的右焦点F分向量

所成的比；若不存在，请说明理由．
（3）（理）当m为定值时，过轨迹C上的点B（m，0）作一条直线l与双曲线E的右支交于不同的两点（图2），且与直线y=

x分别交于M、N两点，求△MON周长的最小值．

已知P（4，4）为圆C：内一定点，圆周上有两个动点

A，B恒有

（1）求弦AB中点M的轨迹方程

（2）以AP和PB为邻边作矩形AQBP，求点Q轨迹方程

（3）若x，y满足Q点轨迹方程，求的最值