题目内容
设α、β是方程x2-2kx+k+6=0的两个实根,则(α-1)2+(β-1)2的最小值是________.
8
分析:由判别式△大于或等于零求出k的范围,由一元二次方程根与系数的关系求得α+β=2k,αβ=k+6,代入要求的式子化简为4• -
-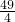 ,故当k=3时,(α-1)2+(β-1)2有最小值,运算求得结果.
,故当k=3时,(α-1)2+(β-1)2有最小值,运算求得结果.
解答:∵α、β是方程x2-2kx+k+6=0的两个实根,
∴判别式△=4k2-4(k+6)=4(k-3)(k+2)≥0,解得 k≥3,或 k≤-2.
且α+β=2k,αβ=k+6,
∴(α-1)2+(β-1)2 =α2+β2-2(α+β )+2=(α+β)2-2αβ-2(α+β )+2=4k2-2(k+6)-2•2k+2=4• -
-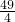 ,
,
故当k=3时,(α-1)2+(β-1)2有最小值是 4• -
-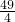 =8,
=8,
故答案为 8.
点评:本题主要考查了一元二次方程的根的分布与系数的关系,二次函数的性质的应用,属于中档题.
分析:由判别式△大于或等于零求出k的范围,由一元二次方程根与系数的关系求得α+β=2k,αβ=k+6,代入要求的式子化简为4•
 -
-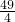 ,故当k=3时,(α-1)2+(β-1)2有最小值,运算求得结果.
,故当k=3时,(α-1)2+(β-1)2有最小值,运算求得结果.解答:∵α、β是方程x2-2kx+k+6=0的两个实根,
∴判别式△=4k2-4(k+6)=4(k-3)(k+2)≥0,解得 k≥3,或 k≤-2.
且α+β=2k,αβ=k+6,
∴(α-1)2+(β-1)2 =α2+β2-2(α+β )+2=(α+β)2-2αβ-2(α+β )+2=4k2-2(k+6)-2•2k+2=4•
 -
-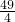 ,
,故当k=3时,(α-1)2+(β-1)2有最小值是 4•
 -
-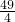 =8,
=8,故答案为 8.
点评:本题主要考查了一元二次方程的根的分布与系数的关系,二次函数的性质的应用,属于中档题.

练习册系列答案
相关题目
设tanα、tanβ是方程x2+3
x+4=0的两根,且α、β∈(-
,
),则α+β的值为( )
| 3 |
| π |
| 2 |
| π |
| 2 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|