题目内容
长方体ABCD-A1B1C1D1中,底面ABCD是边长为2的正方形,高为4,则顶点A1到截面AB1D1的距离为
.
| 4 |
| 3 |
| 4 |
| 3 |
分析:分析:设A1C1∩B1D1=O1,根据线面垂直的判定定理可知B1D1⊥平面AA1O1,再根据面面垂直的判定定理可知故平面AA1O1⊥面AB1D1,交线为AO1,在面AA1O1内过A1作A1H⊥AO1于H,则A1H的长即是点A1到截面AB1D1的距离,在Rt△A1O1A中,利用等面积法求出A1H即可.
解答:解:如图,设A1C1∩B1D1=O1,∵B1D1⊥A1O1,B1D1⊥AA1,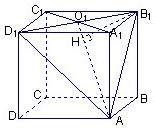
∴B1D1⊥平面AA1O1,
∴平面AA1O1⊥面AB1D1,交线为AO1,
在面AA1O1内过B1作B1H⊥AO1于H,连接A1H,则A1H的长即是点A1到截面AB1D1的距离,
在Rt△A1O1A中,A1O1=
,AO1=3
,
由A1O1•A1A=h•AO1,可得A1H=
故答案为:

∴B1D1⊥平面AA1O1,
∴平面AA1O1⊥面AB1D1,交线为AO1,
在面AA1O1内过B1作B1H⊥AO1于H,连接A1H,则A1H的长即是点A1到截面AB1D1的距离,
在Rt△A1O1A中,A1O1=
| 2 |
| 2 |
由A1O1•A1A=h•AO1,可得A1H=
| 4 |
| 3 |
故答案为:
| 4 |
| 3 |
点评:本题考查点到面的距离的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
长方体ABCD-A1B1C1D1中,AB=3,BC=4,AA1=5 则三棱锥A1-ABC的体积为( )
| A、10 | B、20 | C、30 | D、35 |
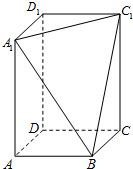 在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.
在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.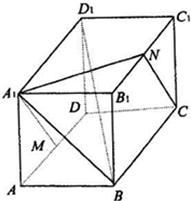 如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC=
如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC= 如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点.
如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点. 在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.
在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.