Question

【题目】如图所示，在四棱锥中，底面是边长为1的菱形，，面，，、分别为、的中点.

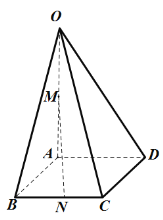
（1）证明：直线平面；

（2）求异面直线与所成角的大小；

（3）求点到平面的距离．

Answer 1

【答案】（1）证明见解析（2）（3）

【解析】

(1) 取的中点，构造平行四边形，再根据线面平行的判定定理完成证明；

(2)根据平行可知异面直线与所成的角即为或其补角，然后根据长度进行求解；

(3)根据线面平行将问题转化为到平面的距离，然后作出在平面内的射影，根据长度即可计算出到平面的距离，即可求解出点到平面的距离.

（1）取的中点，连接、.则四边形为平行四边形，

∴，又∵平面，平面，

∴平面.

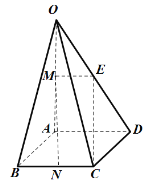
（2）∵，

∴为异面直线与所成的角（或其补角）

作于点，连接.

∵平面，∴，∵，∴.

∵，

∴，.

所以异面直线与所成的角为.

（3）∵平面，∴点和点到平面的距离相等.

连接，过点作于点，

∵，，∴平面，∴，

又∵，∴平面，

线段的长就是点到平面的距离，与点到平面的距离相等

，，

.

所以点到平面的距离为.