题目内容
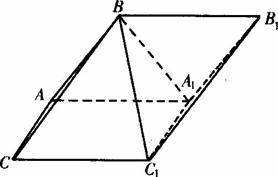
如图，斜三棱柱A1B1C1﹣ABC中，侧面AA1C1C⊥底面ABC，侧面AA1C1C是菱形，
，E、F分别是A1C1、AB的中点．求证：
（1）EF∥平面BB1C1C；
（2）平面CEF⊥平面ABC．
，E、F分别是A1C1、AB的中点．求证：（1）EF∥平面BB1C1C；
（2）平面CEF⊥平面ABC．
证明：（1）取BC中点M，连接FM，C1M，
在△ABC中，因为F，M分别为BA、BC的中点，
所以FM
，
因为E为A1C1的中点，AC
，
所以EF∥EC1，从而四边形EFMC1为平行四边形，
所以EF∥C1M，
又因为C1M?平面BB1C1C，EF?平面BB1C1C，
EF∥平面BB1C1C；
（2）在平面AA1C1C内，作A1O⊥AC，O为垂足，
因为∠A1AC=60°，
所以AO=
AA1=
AC，
从而O为AC的中点．
所以OC
A1E，因而EC
A1O1，
因为侧面AA1C1C⊥底面ABC，交线为AC，A1O⊥AC，
所以A1O⊥面ABC．
所以EC⊥面ABC，
又因为EC
平面EFC，
所以平面CEF⊥平面ABC．
在△ABC中，因为F，M分别为BA、BC的中点，
所以FM
，因为E为A1C1的中点，AC
，所以EF∥EC1，从而四边形EFMC1为平行四边形，
所以EF∥C1M，
又因为C1M?平面BB1C1C，EF?平面BB1C1C，
EF∥平面BB1C1C；
（2）在平面AA1C1C内，作A1O⊥AC，O为垂足，
因为∠A1AC=60°，
所以AO=
AA1=AC，从而O为AC的中点．
所以OC
A1E，因而ECA1O1，因为侧面AA1C1C⊥底面ABC，交线为AC，A1O⊥AC，
所以A1O⊥面ABC．
所以EC⊥面ABC，
又因为EC
平面EFC，所以平面CEF⊥平面ABC．
练习册系列答案
名校课堂系列答案
相关题目
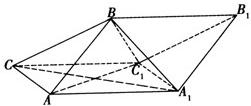如图，斜三棱柱ABC-A1B1C1的侧面AA1C1C是面积为
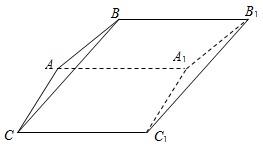如图，斜三棱柱ABC-A1B1C1中，面AA1C1C是菱形，∠ACC1=60°，侧面ABB1A1⊥AA1C1C，A1B=AB=AC=1．求证：
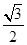的菱形，∠ACC1为锐角，侧面ABB1A1⊥侧面AA1C1C，且A1B=AB=AC=1.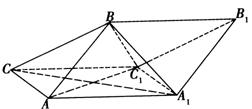
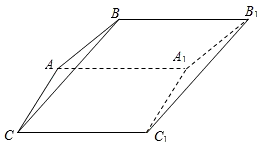如图，斜三棱柱ABC-A1B1C1中，面AA1C1C是菱形，∠ACC1=60°，侧面ABB1A1⊥AA1C1C，A1B=AB=AC=1．
的菱形，∠ACC1为锐角，侧面ABB1A1⊥侧面AA1ClC，A1B=AB=AC=1.