题目内容

过双曲线
x2
a2
-
y2
b2
=1(a＞0，b＞0)的一个焦点F作一条渐线的垂线，垂足为点A，与另一条渐近线交于点B，若
FB
=2
FA
，则此双曲线的离心率为（　　）
A、
2
B、
3
C、2
D、
5
分析：先由
FB
=2
FA
，得出A为线段FB的中点，再借助于图象分析出其中一条渐近线对应的倾斜角的度数，找到a，b之间的等量关系，进而求出双曲线的离心率．
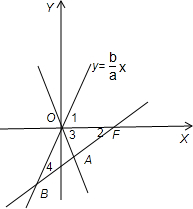解答：精英家教网解：如图因为
FB
=2
FA
，所以A为线段FB的中点，
∴∠2=∠4，又∠1=∠3，∠2+∠3=90°，所以∠1=∠2+∠4=2∠2=∠3．
故∠2+∠3=90°=3∠2?∠2=30°?∠1=60°?
b
a
=
3
．
∴e2=1+(
b
a
)2=4?e=2．
故选C．
点评：本题是对双曲线的渐近线以及离心率的综合考查，是考查基本知识，属于基础题．
练习册系列答案
相关题目
过双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的一个焦点F引它的渐近线的垂线，垂足为M，延长FM交y轴于E，若FM=ME，则该双曲线的离心率为（　　）
A、3
B、2
C、
3
D、
2
过双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的右焦点F作圆x2+y2=a2的切线FM（切点为M），交y轴于点P．若M为线段FP的中点，则双曲线的离心率是
 
．
过双曲线
x2
a2
-
y2
b2
=1的左焦点F作⊙O：x2+y2=a2的两条切线，记切点为A，B，双曲线左顶点为C，若∠ACB=120°，则双曲线的渐近线方程为（　　）
A、y=±
3
x
B、y=±
3
3
x
C、y=±
2
x
D、y=±
2
2
x
过双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的一个焦点F引它到渐进线的垂线，垂足为M，延长FM交y轴于E，若
FM
=2
ME
，则该双曲线离心率为（　　）
过双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的一个焦点F作一条渐近线的平行线，该平行线与y轴交于点P，若|OP|=|OF|，则双曲线的离心率为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网