Question

【题目】如图，在正方形ABCD中，E为AB的中点，P为以A为圆心、AB为半径的圆弧上的任意一点，设向量 ，则λ+μ的最小值为 ．

Answer 1

【答案】
【解析】解：以A为原点，以AB所在的为x轴，建立坐标系，设正方形ABCD的边长为1， 则E（ ，0），C（1，1），D（0，1），A（0，0），B（1，0）．
设 P（cosθ，sinθ），∴ =（1，1）．
再由向量 =λ（ ，﹣1）+μ（cosθ，sinθ）=（ ，﹣λ+μsinθ ）=（1，1），
∴ ，∴ ，
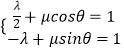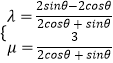∴λ+μ= = =﹣1+ ．
由题意得 0≤θ≤ ，∴0≤cosθ≤1，0≤sinθ≤1．
求得（λ+μ）′= = ＞0，
故λ+μ在[0， ]上是增函数，故当θ=0时，即cosθ=1，这时λ+μ取最小值为 = ，
故答案为： ．
建立坐标系，设正方形ABCD的边长为1，求出向量 =（ ，﹣λ+μsinθ ）=（1，1），用cosθ，sinθ表示 λ和μ，根据cosθ，sinθ 的取值范围，再结合λ+μ的单调性，求出λ+μ= 的最小值．