题目内容
已知命题p:方程mx2+4y2=4m(m∈R)表示焦点在y轴上的椭圆,命题q:?x∈R,cosx-m>0恒成立.若p∨q为假命题,则实数m的取值范围是 .
分析:分别求出命题p,q为真命题的等价条件,然后利用p∨q为假命题,确定条件关系,即可求m的取值范围.
解答:解:方程mx2+4y2=4m(m∈R)表示焦点在y轴上的椭圆,
则m≠0,椭圆的标准方程为
+
=1,
则m>4.
即命题p真时,m>4,则p假时,m≤4;
若?x∈R,cosx-m>0恒成立,
则m<cosx,∴m<-1,
命题q真时,m<-1,命题q假时,m≥-1,
若p∨q为假命题,则p假q假,
即
,即-1≤m≤4.
故实数m的取值范围是-1≤m≤4.
故答案为:-1≤m≤4.
则m≠0,椭圆的标准方程为
| x2 |
| 4 |
| y2 |
| m |
则m>4.
即命题p真时,m>4,则p假时,m≤4;
若?x∈R,cosx-m>0恒成立,
则m<cosx,∴m<-1,
命题q真时,m<-1,命题q假时,m≥-1,
若p∨q为假命题,则p假q假,
即
|
故实数m的取值范围是-1≤m≤4.
故答案为:-1≤m≤4.
点评:本题主要考查复合命题与简单命题之间的关系,利用条件求出命题p,q为真的等价条件是解决本题的关键.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
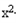 +mx+1=0有两上不相等的负实根,命题q:不等式4
+mx+1=0有两上不相等的负实根,命题q:不等式4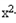 +4(m﹣2)x+1>0的解集为R,若p∨q为真命题,p∧q为假命题,求m的取值范围.
+4(m﹣2)x+1>0的解集为R,若p∨q为真命题,p∧q为假命题,求m的取值范围.