题目内容
(本小题满分14分)
已 知直线
知直线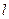 :
: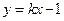 与圆
与圆 :
: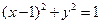 相交于
相交于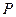 、
、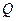 两点,点
两点,点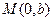 满足
满足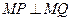 .
.
(Ⅰ)当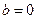 时,求实数
时,求实数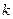 的值;
的值;
(Ⅱ)当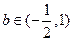 时,求实数
时,求实数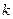 的取值范围;
的取值范围;
(Ⅲ)设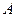 、
、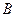 是圆
是圆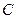 :
: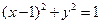 上两点,且满足
上两点,且满足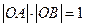 ,试问:是否存在一个定圆
,试问:是否存在一个定圆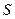 ,使直线
,使直线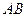 恒与圆
恒与圆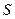 相切.
相切.
已
 知直线
知直线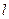 :
: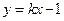 与圆
与圆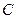 :
: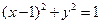 相交于
相交于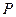 、
、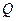 两点,点
两点,点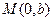 满足
满足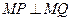 .
.(Ⅰ)当
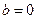 时,求实数
时,求实数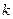 的值;
的值;(Ⅱ)当
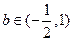 时,求实数
时,求实数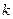 的取值范围;
的取值范围;(Ⅲ)设
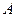 、
、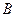 是圆
是圆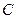 :
: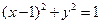 上两点,且满足
上两点,且满足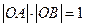 ,试问:是否存在一个定圆
,试问:是否存在一个定圆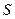 ,使直线
,使直线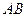 恒与圆
恒与圆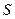 相切.
相切.解:(Ⅰ)当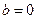 时,点
时,点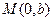 在圆
在圆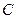 上,当且仅当直线
上,当且仅当直线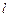 经过圆心
经过圆心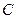 时,满足
时,满足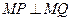 .
.
∵圆心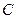 的坐标为
的坐标为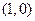 ,代入直线
,代入直线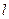 的方程
的方程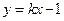 ,得
,得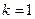 . ………………3分
. ………………3分
(Ⅱ)设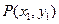 ,
,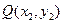 ,
,
由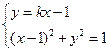 ,
,
消去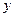 ,得
,得 .
.
于是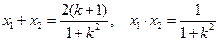 .………………4分
.………………4分
∵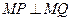 ,∴
,∴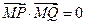 .
.
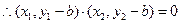 ,即
,即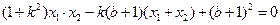 .
.
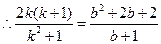 ,
,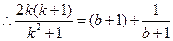 .………………6分
.………………6分
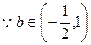 ,
,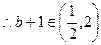 .
.
令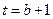 ,则
,则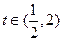 .
.
令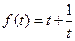 ,
,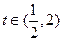 ,设
,设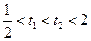 ,
,
则 ,
,
∴当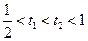 时,函数
时,函数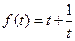 单调递减;
单调递减;
当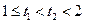 时,函数
时,函数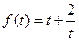 单调递增.
单调递增.
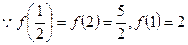 ,
,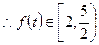 .………………8分
.………………8分
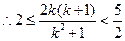 ,解得
,解得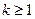 .
.
所以k的取值范围为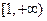 . ……………………9分
. ……………………9分

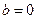 时,点
时,点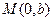 在圆
在圆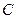 上,当且仅当直线
上,当且仅当直线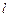 经过圆心
经过圆心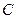 时,满足
时,满足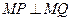 .
.∵圆心
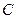 的坐标为
的坐标为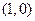 ,代入直线
,代入直线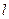 的方程
的方程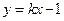 ,得
,得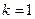 . ………………3分
. ………………3分(Ⅱ)设
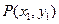 ,
,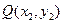 ,
,由
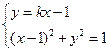 ,
,消去
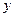 ,得
,得 .
.于是
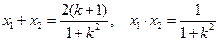 .………………4分
.………………4分∵
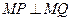 ,∴
,∴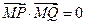 .
.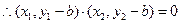 ,即
,即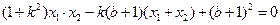 .
.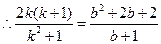 ,
,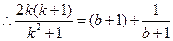 .………………6分
.………………6分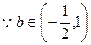 ,
,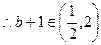 .
.令
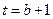 ,则
,则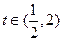 .
.令
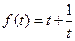 ,
,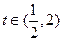 ,设
,设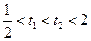 ,
,则
 ,
,∴当
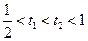 时,函数
时,函数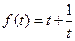 单调递减;
单调递减;当
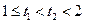 时,函数
时,函数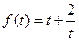 单调递增.
单调递增.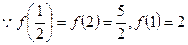 ,
,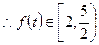 .………………8分
.………………8分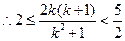 ,解得
,解得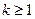 .
.所以k的取值范围为
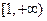 . ……………………9分
. ……………………9分
略

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 应该使它与球有最大的接触面积,问圆轴的半径x应是多少?
应该使它与球有最大的接触面积,问圆轴的半径x应是多少?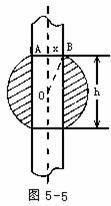
 :
: 与
与 轴交于点
轴交于点 、
、
 ,与
,与 轴交于点
轴交于点 ,其中
,其中
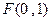 ,一动圆过点
,一动圆过点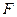 且与圆
且与圆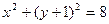 内切.
内切.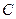 的方程;
的方程;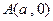 ,点
,点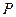 为曲线
为曲线 任一点,求点
任一点,求点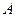 到点
到点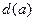 ;
;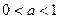 的条件下,设△
的条件下,设△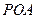 的面积为
的面积为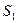 (
(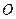 是坐标原点,
是坐标原点,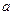 的点),以
的点),以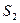 .若正数
.若正数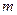 使得
使得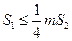 恒成立,问
恒成立,问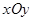 中,已知圆
中,已知圆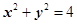 上有且仅有四个点到直线
上有且仅有四个点到直线 的距离为1,则实数c的取值范围是_________
的距离为1,则实数c的取值范围是_________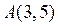 的圆的切线方程;
的圆的切线方程;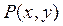 为圆上任意一点,求
为圆上任意一点,求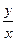 的最值。
的最值。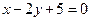 与圆
与圆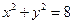 相交于A、B两点,则
相交于A、B两点,则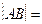 ▲ 。
▲ 。 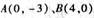 ,若点P是圆
,若点P是圆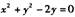 上的动点,ΔABP面积的最小值为
上的动点,ΔABP面积的最小值为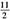 c. 8 d.
c. 8 d.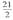
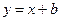 与曲线
与曲线 有且仅有一个公共点,则b的取值范围是 .
有且仅有一个公共点,则b的取值范围是 .