题目内容
设函数 ,
,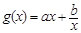 ,函数
,函数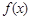 的图象与
的图象与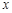 轴的交点也在函数
轴的交点也在函数 的图象上,且在此点有公切线.
的图象上,且在此点有公切线.
(Ⅰ)求 ,
,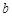 的值;
的值;
(Ⅱ)试比较 与
与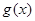 的大小.
的大小.
【答案】
(Ⅰ) ,
, ;(Ⅱ)当
;(Ⅱ)当 时,
时,  ;当
;当 时,
时,  .
.
【解析】
试题分析:(Ⅰ)先求交点,代入可得 ,然后求导数,根据导数的几何意义可得
,然后求导数,根据导数的几何意义可得 ,联立解得
,联立解得 ,
, ;(Ⅱ)利用作差法,然后分析差值函数的导数的正负分析原函数的单调性.
;(Ⅱ)利用作差法,然后分析差值函数的导数的正负分析原函数的单调性.
试题解析:(Ⅰ) 的图象与
的图象与 轴的交点坐标是
轴的交点坐标是 ,
,
依题意,得 ①
1分
①
1分
又 ,
, ,
, 
 与
与 在点
在点 处有公切线,
处有公切线,
∴ 即
即 ② 4分
② 4分
由①、②得 ,
, 5分
5分
(Ⅱ)令 ,则
,则

∴
∴ 在
在 上为减函数
6分
上为减函数
6分
当 时,
时, ,即
,即 ;
;
当 时,
时, ,即
,即 ;
;
当 时,
时, ,即
,即 .
.
综上可知,当 时,即
时,即 ;当
;当 时,即
时,即 . 12分
. 12分
考点:1.导数公式;2.导数的几何意义;3.函数的单调性.

练习册系列答案
相关题目
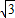 sin2x),x∈R.
sin2x),x∈R.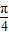 ,0],求函数f(x)的值域;
,0],求函数f(x)的值域;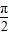 )平移后得到函数y=2sin2x的图象,求实数m、n的值.
)平移后得到函数y=2sin2x的图象,求实数m、n的值. ,有下列结论:①点
,有下列结论:①点 是函数
是函数 图象的一个对称中心;②直线
图象的一个对称中心;②直线 是函数
是函数 个单位后,对应的函数是偶函数。其中所有正确结论的序号是
。
个单位后,对应的函数是偶函数。其中所有正确结论的序号是
。 ,
, ,函数
,函数
 轴的交点也在函数
轴的交点也在函数


 的大小.
的大小.