题目内容
(本小题满分12分)
设函数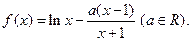
(Ⅰ)若函 数
数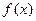 在其定义域内是增函数,求
在其定义域内是增函数,求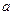 的取值范围;
的取值范围;
(Ⅱ)设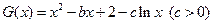 ,方程
,方程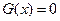 有两根
有两根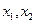 ,记
,记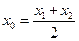 .试探究
.试探究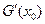 值的符号,其中
值的符号,其中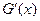 是
是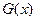 的导函数.
的导函数.
设函数
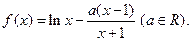
(Ⅰ)若函
 数
数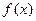 在其定义域内是增函数,求
在其定义域内是增函数,求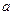 的取值范围;
的取值范围;(Ⅱ)设
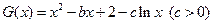 ,方程
,方程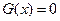 有两根
有两根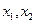 ,记
,记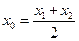 .试探究
.试探究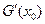 值的符号,其中
值的符号,其中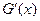 是
是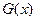 的导函数.
的导函数.解:(Ⅰ)(解法1)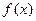 的定义域是
的定义域是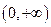 .
.
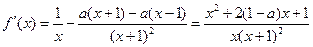 ………………2分
………………2分
要使函数在定义域内是增函数,只要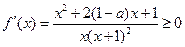 ,在
,在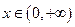 恒成立,即
恒成立,即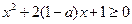 在
在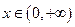 恒成立,
恒成立,
所以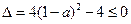 或
或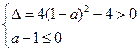 ……………4分
……………4分
解得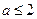 .………………6分
.………………6分
解法(2)由解法1,只要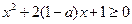 在
在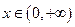 恒成立,
恒成立,
即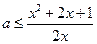 在
在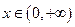 恒成立,所以
恒成立,所以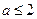 .
.
(Ⅱ)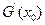 的符号为正.
的符号为正.
理由为:因为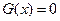 有两个零点
有两个零点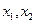 ,则有
,则有
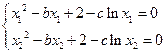 ,两式相减得
,两式相减得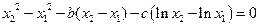
即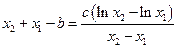 ,………………8分
,………………8分
于是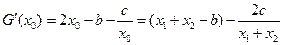
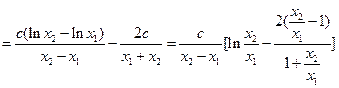 ………………10分
………………10分
①当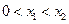 时,令
时,令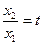 ,则
,则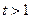 ,且
,且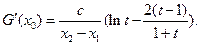
设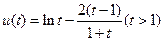 ,由(Ⅰ)知
,由(Ⅰ)知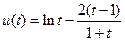 在
在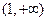 上为增函数.而
上为增函数.而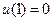 ,所以
,所以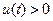 ,即
,即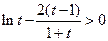 . 又因为
. 又因为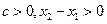 ,所以
,所以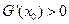 .
.
②当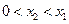 时,同理可得:
时,同理可得: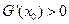 . 综上所述:
. 综上所述: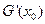 的符号为正.……12分
的符号为正.……12分
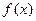 的定义域是
的定义域是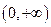 .
.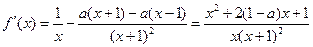 ………………2分
………………2分要使函数在定义域内是增函数,只要
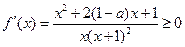 ,在
,在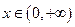 恒成立,即
恒成立,即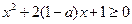 在
在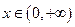 恒成立,
恒成立, 所以
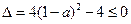 或
或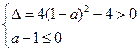 ……………4分
……………4分解得
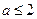 .………………6分
.………………6分解法(2)由解法1,只要
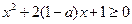 在
在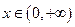 恒成立,
恒成立,即
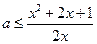 在
在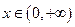 恒成立,所以
恒成立,所以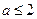 .
.(Ⅱ)
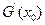 的符号为正.
的符号为正. 理由为:因为
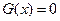 有两个零点
有两个零点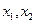 ,则有
,则有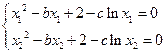 ,两式相减得
,两式相减得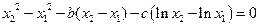
即
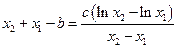 ,………………8分
,………………8分于是
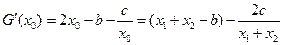
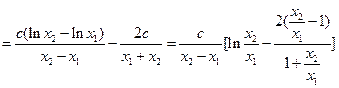 ………………10分
………………10分①当
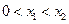 时,令
时,令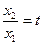 ,则
,则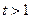 ,且
,且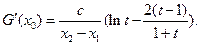
设
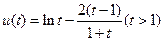 ,由(Ⅰ)知
,由(Ⅰ)知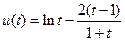 在
在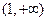 上为增函数.而
上为增函数.而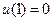 ,所以
,所以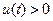 ,即
,即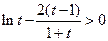 . 又因为
. 又因为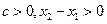 ,所以
,所以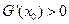 .
.②当
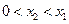 时,同理可得:
时,同理可得: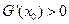 . 综上所述:
. 综上所述: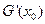 的符号为正.……12分
的符号为正.……12分略

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
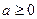 ,函数
,函数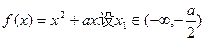 ,记曲线
,记曲线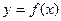 在点
在点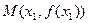 处切线为
处切线为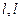 与x轴的交点是
与x轴的交点是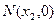 ,O为坐标原点。
,O为坐标原点。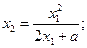
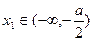 ,都
,都 有
有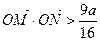 成立,求a的取值范围。
成立,求a的取值范围。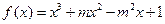
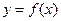 的切线,求此直线方程.
的切线,求此直线方程.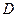 上的函数
上的函数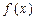 ,如果满足:对任意
,如果满足:对任意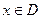 ,存在常数
,存在常数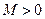 ,都有
,都有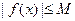 成立,则称
成立,则称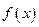 是
是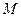 称为函数
称为函数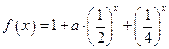 ;
;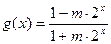 .
. 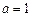 时,求函数
时,求函数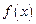 在
在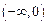 上的值域,并判断函数
上的值域,并判断函数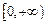 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数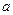 的取值范围;
的取值范围;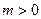 ,函数
,函数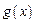 在
在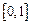 上的上界是
上的上界是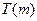 ,求
,求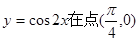 处的切线方程是( )
处的切线方程是( )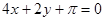
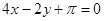
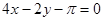
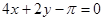
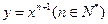 在点(1,1)处的切线与x轴的交点的横坐标为
在点(1,1)处的切线与x轴的交点的横坐标为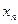 ,
,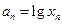 ,则
,则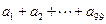 的值为 .
的值为 . 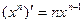 ,
,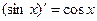 ,
,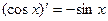 ,是否可判断,可导的奇函数的导函数是偶函数,可导的偶函数的导函数是奇函数。
,是否可判断,可导的奇函数的导函数是偶函数,可导的偶函数的导函数是奇函数。 ―3x2―12x+5在[0,3]上的最大值、最小值分别是 ( )
―3x2―12x+5在[0,3]上的最大值、最小值分别是 ( )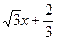 上的任意一点,P点处切线倾斜角为α,则角α的取值范围是 。
上的任意一点,P点处切线倾斜角为α,则角α的取值范围是 。