题目内容
当_________时,
成立.
解析：要成立,就是使
-b＜a-b成立,即使
成立,
即使ab2＜a2b成立.
由ab2-a2b＜0,得ab(b-a)＜0.
∴当ab＞0且b＜a或ab＜0且b＞a时原不等式成立.
答案：ab＞0且a＞b或ab＜0且b＞a
练习册系列答案
相关题目
等式12+22+32+…+n2=
（ ）
| 5n2-7n+4 |
| 2 |
| A、n为任何自然数时都成立 |
| B、仅当n=1，2，3时成立 |
| C、n=4时成立，n=5时不成立 |
| D、仅当n=4时不成立 |
证明1+
+
+
+…+
＞
（n∈N*），假设n=k时成立，当n=k+1时，左端增加的项数是（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2n-1 |
| n |
| 2 |
| A、1项 |
| B、k-1项 |
| C、k项 |
| D、2k项 |
∥
，
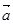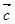，则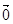
时成立 C.当