题目内容
对于连续函数f(x)和g(x),函数|f(x)-g(x)|在闭区间[a,b]上的最大值称为f(x)与g(x)在闭区间[a,b]上的“绝对差”,记为
b(f(x),g(x)),则
4(
,
x2-x)=______.
| △ |
| a≤x≤ |
| △ |
| 1≤x≤ |
| 1 |
| x+1 |
| 2 |
| 9 |
设h(x)=
-
x2+x,x∈[1,4]
所以h′(x)=-
-
x+1,x∈[1,4]
令h′(x)>0解得1<x<2,令h′(x)<0解得2<x<4.
所以h(x)在[1,4]上先增后减.
所以h(x)的最值在x=1或x=2或x=4处取得,
h(1)=
,h(2)=
,h(4)=
,
所以h(x)∈[
,
]
故答案为:
.
| 1 |
| x+1 |
| 2 |
| 9 |
所以h′(x)=-
| 1 |
| (x+1)2 |
| 4 |
| 9 |
令h′(x)>0解得1<x<2,令h′(x)<0解得2<x<4.
所以h(x)在[1,4]上先增后减.
所以h(x)的最值在x=1或x=2或x=4处取得,
h(1)=
| 23 |
| 18 |
| 13 |
| 9 |
| 29 |
| 45 |
所以h(x)∈[
| 29 |
| 45 |
| 13 |
| 9 |
故答案为:
| 13 |
| 9 |

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
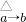 (f(x),g(x)).若
(f(x),g(x)).若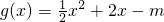 ,且
,且 (f(x),g(x))=
(f(x),g(x))= ,求m的值.
,求m的值.