题目内容
如图的正方体ABCD-A′B′C′D′中，异面直线AA′与BC所成的角是
- A.30°
- B.45°
- C.60°
- D.90°
D
分析：由题意即正方体图形，利用正方形的特点．由于AD∥BC，利用异面直线的定义即可得求．
解答：根据题意，如图示的正方体ABCD-A′B′C′D′中，易得∠A′AD=90°．
∵AD∥BC
∴异面直线AA′与BC垂直，即所成的角为90°，
故答案选：D．
点评：此题考查了异慢直线见的定义，还考查了正方体的特点．
分析：由题意即正方体图形，利用正方形的特点．由于AD∥BC，利用异面直线的定义即可得求．
解答：根据题意，如图示的正方体ABCD-A′B′C′D′中，易得∠A′AD=90°．
∵AD∥BC
∴异面直线AA′与BC垂直，即所成的角为90°，
故答案选：D．
点评：此题考查了异慢直线见的定义，还考查了正方体的特点．
练习册系列答案
相关题目
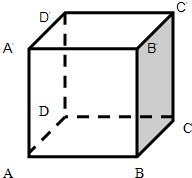3、如图的正方体ABCD-A′B′C′D′中，异面直线AA′与BC所成的角是（ ）
10、如图的正方体ABCD-A1B1C1D1中，异面直线A1B与B1C所成的角是（ ）
在如图的正方体ABCD-A1B1C1D1中，直线AC1与平面CB1D1所成的角为
如图的正方体ABCD-A1B1C1D1中，异面直线A1B与B1C所成的角是（ ）