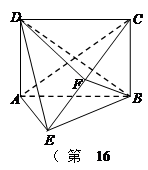题目内容
如图1,在边长为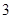 的正三角形
的正三角形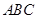 中,
中,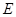 ,
,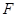 ,
,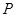 分别为
分别为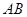 ,
,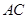 ,
,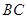 上的点,且满足
上的点,且满足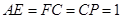 .将△
.将△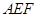 沿
沿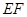 折起到△
折起到△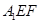 的位置,使二面角
的位置,使二面角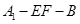 成直二面角,连结
成直二面角,连结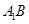 ,
,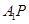 .(如图2)
.(如图2)

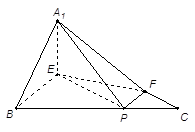
(Ⅰ)求证: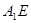 ⊥平面
⊥平面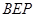 ;
;
(Ⅱ)求直线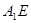 与平面
与平面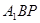 所成角的大小.
所成角的大小.
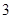 的正三角形
的正三角形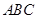 中,
中,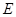 ,
,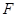 ,
,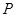 分别为
分别为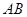 ,
,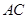 ,
,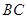 上的点,且满足
上的点,且满足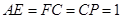 .将△
.将△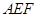 沿
沿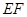 折起到△
折起到△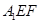 的位置,使二面角
的位置,使二面角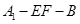 成直二面角,连结
成直二面角,连结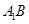 ,
,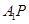 .(如图2)
.(如图2)
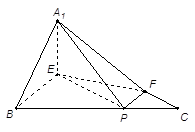
(Ⅰ)求证:
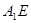 ⊥平面
⊥平面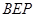 ;
;(Ⅱ)求直线
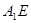 与平面
与平面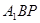 所成角的大小.
所成角的大小.(Ⅰ)证明见解析;(Ⅱ)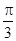 .
.
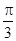 .
.(I)在平面图形中证明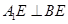 ,
,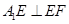 即可.
即可.
(2)可以采用空间向量法求解,求出平面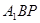 的法向量
的法向量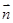 ,那么
,那么 与
与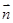 的夹角(锐角)与所求线面角互余.
的夹角(锐角)与所求线面角互余.
(Ⅰ)证明:取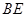 中点
中点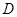 ,连结
,连结
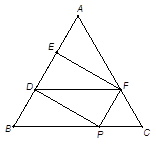
因为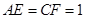 ,
,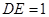 ,
,
所以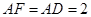 ,而
,而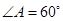 ,即△
,即△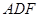 是正三角形.又因为
是正三角形.又因为 , 所以
, 所以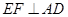 .所以在图2中有
.所以在图2中有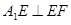 ,
,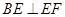 .
.
所以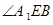 为二面角
为二面角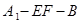 的平面角.
的平面角.
又二面角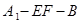 为直二面角, 所以
为直二面角, 所以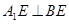 .
.
又因为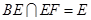 , 所以
, 所以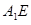 ⊥平面
⊥平面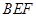 ,即
,即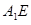 ⊥平面
⊥平面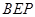 .
.
(Ⅱ)解:由(Ⅰ)可知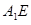 ⊥平面
⊥平面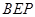 ,
,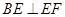 ,如图,以
,如图,以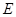 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系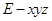 ,
,
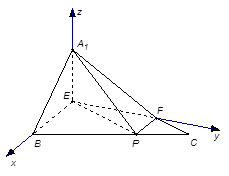
则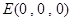 ,
,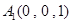 ,
,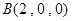 ,
,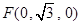 .
.
在图1中,连结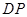 .因为
.因为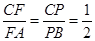 ,
,
所以 ∥
∥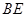 ,且
,且 .所以四边形
.所以四边形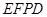 为平行四边形.
为平行四边形.
所以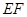 ∥
∥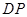 ,且
,且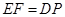 .
.
故点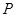 的坐标为(1,
的坐标为(1,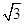 ,0).图2
,0).图2
所以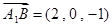 ,
,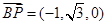 ,
,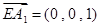
不妨设平面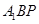 的法向量
的法向量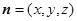 ,则
,则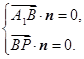
即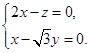 令
令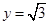 ,得
,得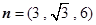 .
.
所以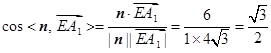
故直线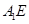 与平面
与平面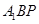 所成角的大小为
所成角的大小为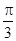 .
.
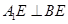 ,
,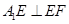 即可.
即可.(2)可以采用空间向量法求解,求出平面
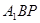 的法向量
的法向量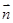 ,那么
,那么 与
与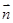 的夹角(锐角)与所求线面角互余.
的夹角(锐角)与所求线面角互余.(Ⅰ)证明:取
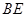 中点
中点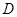 ,连结
,连结
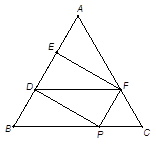
因为
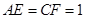 ,
,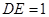 ,
,所以
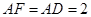 ,而
,而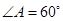 ,即△
,即△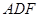 是正三角形.又因为
是正三角形.又因为 , 所以
, 所以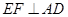 .所以在图2中有
.所以在图2中有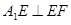 ,
,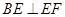 .
. 所以
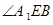 为二面角
为二面角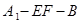 的平面角.
的平面角. 又二面角
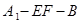 为直二面角, 所以
为直二面角, 所以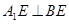 .
. 又因为
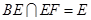 , 所以
, 所以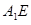 ⊥平面
⊥平面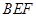 ,即
,即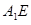 ⊥平面
⊥平面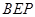 .
. (Ⅱ)解:由(Ⅰ)可知
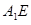 ⊥平面
⊥平面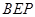 ,
,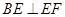 ,如图,以
,如图,以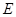 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系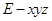 ,
,
则
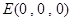 ,
,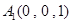 ,
,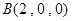 ,
,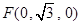 .
.在图1中,连结
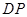 .因为
.因为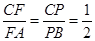 ,
,所以
 ∥
∥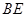 ,且
,且 .所以四边形
.所以四边形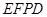 为平行四边形.
为平行四边形.所以
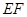 ∥
∥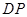 ,且
,且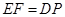 .
.故点
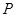 的坐标为(1,
的坐标为(1,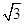 ,0).图2
,0).图2所以
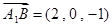 ,
,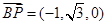 ,
,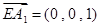
不妨设平面
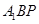 的法向量
的法向量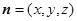 ,则
,则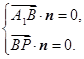
即
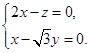 令
令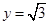 ,得
,得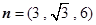 .
.所以
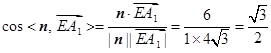
故直线
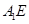 与平面
与平面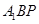 所成角的大小为
所成角的大小为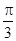 .
.
练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
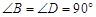 ,
,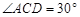 ,
,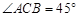 ,
,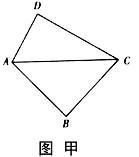
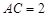 ,现将三角板
,现将三角板 沿
沿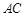 折起,使
折起,使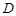 在平面
在平面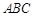 上的射影恰好在
上的射影恰好在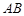 上,如图乙.
上,如图乙.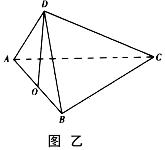
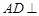 平面
平面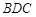 ;
; 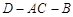 的余弦值;
的余弦值;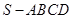 中,底面
中,底面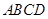 是正方形,其他四个侧面都是等边三角形,
是正方形,其他四个侧面都是等边三角形,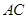 与
与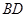 的交点为
的交点为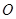 ,
,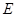 为侧棱
为侧棱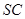 上一点.
上一点.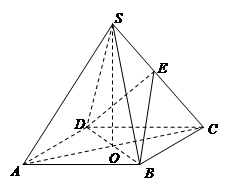
 ,则
,则
 是直二面角,若直线
是直二面角,若直线 则
则
 在平面
在平面 ,则
,则 或
或
 ,则n与
,则n与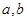 是不同的直线,
是不同的直线,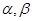 是不同的平面,则下列结论错误的是( )
是不同的平面,则下列结论错误的是( )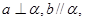 则
则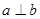
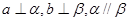 ,则
,则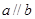
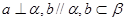 ,则
,则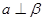
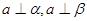 ,则
,则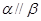
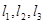 是空间三条不同的直线,则下列命题正确的是( )
是空间三条不同的直线,则下列命题正确的是( )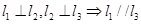
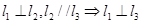
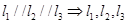 共面
共面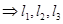 共面
共面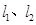 为异面直线,直线
为异面直线,直线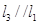 ,则
,则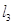 与
与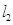 的位置关系是
的位置关系是 中,底面
中,底面 为矩形,平面
为矩形,平面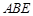 ,
,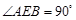 ,
,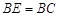 ,
,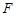 为
为 的中点,
的中点,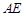 ∥平面
∥平面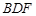 ;(2)平面
;(2)平面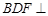 平面
平面 .
.