题目内容
【题目】某超市从![]() 年甲、乙两种酸奶的日销售量(单位:箱)的数据中分别随机抽取
年甲、乙两种酸奶的日销售量(单位:箱)的数据中分别随机抽取![]() 个,并按
个,并按![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分组,得到频率分布直方图如图,假设甲、乙两种酸奶独立销售且日销售量相互独立.
分组,得到频率分布直方图如图,假设甲、乙两种酸奶独立销售且日销售量相互独立.
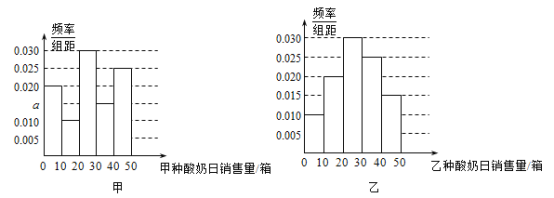
(1)写出频率分布直方图甲中的![]() 的值;记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为
的值;记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为![]() 、
、![]() ,试比较
,试比较![]() 与
与![]() 的大小;(只需写出结论)
的大小;(只需写出结论)
(2)估计在未来的某一天里,甲、乙两种酸奶的销售量恰有一个高于![]() 箱且另一个不高于
箱且另一个不高于![]() 箱的概率;
箱的概率;
(3)设![]() 表示在未来
表示在未来![]() 天内甲种酸奶的日销售量不高于
天内甲种酸奶的日销售量不高于![]() 箱的天数,以日留住量落入各组的频率为概率,求
箱的天数,以日留住量落入各组的频率为概率,求![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)分布列见解析,数学期望为
;(3)分布列见解析,数学期望为![]() .
.
【解析】
(1)由各小矩形面积和为![]() ,先求出
,先求出![]() ,由频率分布直方图可看出,甲的销售量比较分散,而乙较为集中,由此能比
,由频率分布直方图可看出,甲的销售量比较分散,而乙较为集中,由此能比![]() 、
、![]() 的大小;
的大小;
(2)分两种情况讨论:甲种酸奶的销售量高于![]() 箱,乙种酸奶的销售量不高于
箱,乙种酸奶的销售量不高于![]() 箱;甲种酸奶的销售量不高于
箱;甲种酸奶的销售量不高于![]() 箱,乙种酸奶的销售量高于
箱,乙种酸奶的销售量高于![]() 箱.然后利用独立事件的概率乘法公式可计算出所求事件的概率;
箱.然后利用独立事件的概率乘法公式可计算出所求事件的概率;
(3)由题意得出![]() ,利用二项分布可得出随机变量
,利用二项分布可得出随机变量![]() 的分布列,并计算出随机变量
的分布列,并计算出随机变量![]() 的数学期望.
的数学期望.
(1)由各小矩形面积和为![]() ,得
,得![]() ,解得
,解得![]() ,
,
由频率分布直方图可看出,甲的销售量比较分散,而乙较为集中,主要集中在![]() 箱,故
箱,故![]() ;
;
(2)设事件![]() :在未来的某一天里,甲种酸奶的销售量不高于
:在未来的某一天里,甲种酸奶的销售量不高于![]() 箱;
箱;
事件![]() :在未来的某一天里,乙种酸奶的销售量不高于
:在未来的某一天里,乙种酸奶的销售量不高于![]() 箱;
箱;
事件![]() :在未来的某一天里,甲、乙两种酸奶的销售量恰好一个高于
:在未来的某一天里,甲、乙两种酸奶的销售量恰好一个高于![]() 箱且另一个不高于
箱且另一个不高于![]() 箱.
箱.
则![]() ,
,![]() ,
,
![]() ;
;
(3)由题意可知,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
所以,随机变量![]() 的分布列如下表所示:
的分布列如下表所示:
|
|
|
|
|
|
|
|
|
|
随机变量![]() 的数学期望为
的数学期望为![]() .
.

【题目】在一次期末数学测试中,唐老师任教班级学生的考试得分情况如表所示:
分数区间 |
|
|
|
|
|
人数 | 2 | 8 | 32 | 38 | 20 |
(1)根据上述表格,试估计唐老师所任教班级的学生在本次期末数学测试的平均成绩;
(2)现从成绩在![]() 中按照分数段,采取分层抽样的方法随机抽取5人,再在这5人中随机抽取2人作小题得分分析,求恰有1人的成绩在
中按照分数段,采取分层抽样的方法随机抽取5人,再在这5人中随机抽取2人作小题得分分析,求恰有1人的成绩在![]() 上的概率.
上的概率.