题目内容
 某工厂对一批产品进行了抽样检测,右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36.
某工厂对一批产品进行了抽样检测,右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36.(1)求样本容量及样本中净重大于或等于98克并且小于104克的产品的个数;
(2)已知这批产品中每个产品的利润y(单位:元)与产品净重x(单位:克)的关系式为y=
|
分析:(1)根据频率直方图的意义,由样本中净重在[96,100)的产品个数是36可求样本容量,进而得出样本中净重在[98,104)的产品个数.
(2)先根据频率分布图得出产品净重分组为[96,98),[98,104),[104,106]的频率,从而得到其相应的频数,再结合利润y(单位:元)与产品净重x(单位:克)的关系式即可求出这批产品平均每个的利润.
(2)先根据频率分布图得出产品净重分组为[96,98),[98,104),[104,106]的频率,从而得到其相应的频数,再结合利润y(单位:元)与产品净重x(单位:克)的关系式即可求出这批产品平均每个的利润.
解答:解:(1)由题意可知:样本中净重在[96,100)的产品的频率=(0.05+0.1)×2=0.3,
∴样本容量=
=120,
∴样本中净重在[98,104)的产品个数=(0.1+0.15+0.125)×2×120=90.
(2)产品净重分组为[96,98),[98,104),[104,106]的频率分别为
0.050×2,(0.100+0.015+0.0125)×2,0.075×2,即0.100,0.750,0.150.
∴其相应的频数分别为0.100×120,0.750×120,0.150×120,即12,90,18.
∴这批产品平均每个的利润为
×(12×3+90×5+18×4)=4.65(元).
∴样本容量=
| 36 |
| 0.3 |
∴样本中净重在[98,104)的产品个数=(0.1+0.15+0.125)×2×120=90.
(2)产品净重分组为[96,98),[98,104),[104,106]的频率分别为
0.050×2,(0.100+0.015+0.0125)×2,0.075×2,即0.100,0.750,0.150.
∴其相应的频数分别为0.100×120,0.750×120,0.150×120,即12,90,18.
∴这批产品平均每个的利润为
| 1 |
| 120 |
点评:本题是对频率分布直方图、频率、频数运用的简单考查,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
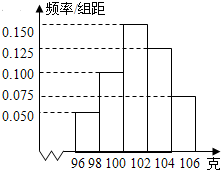 某工厂对一批产品进行了抽样检测.如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )
某工厂对一批产品进行了抽样检测.如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )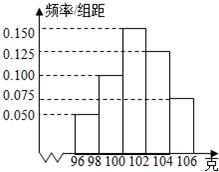 某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是
某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是 (2013•闵行区二模)某工厂对一批产品进行抽样检测,根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图如图所示,已知产品净重的范围是区间[96,106],样本中净重在区间[96,100)的产品个数是24,则样本中净重在区间[100,104)的产品个数是
(2013•闵行区二模)某工厂对一批产品进行抽样检测,根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图如图所示,已知产品净重的范围是区间[96,106],样本中净重在区间[96,100)的产品个数是24,则样本中净重在区间[100,104)的产品个数是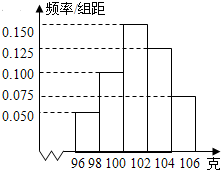 某工厂对一批产品进行了抽样检测,右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[l04,l06].已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于102克的产品的个数是( )
某工厂对一批产品进行了抽样检测,右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[l04,l06].已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于102克的产品的个数是( )