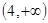题目内容
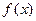 是定义在
是定义在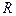 上的以3为周期的偶函数
上的以3为周期的偶函数 ,且
,且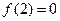 ,则方程
,则方程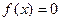 在区间
在区间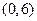 内解的个数的最小值是 ( )
内解的个数的最小值是 ( )
| A.5 | B.4 | C.3 | D.2 |
B
解析

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若函数 为奇函数,则a=
为奇函数,则a=
A.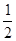 | B.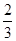 | C.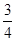 | D.1 |
若函数f(x)=在(0,+∞)上为增函数,则a的取值范围是( )
| A.(-∞,0) | B.(0,+∞) |
| C.R | D.[-1,1] |
已知函数 函数
函数 ,若存在
,若存在 ,使得
,使得 成立,则实
成立,则实
数 的取值范围是
的取值范围是
A. | B. | C. | D. |
已知函数 ,则
,则 的值是
的值是
A. | B. | C. | D. |
设 ,则此函数在区间(0,1)内为( )
,则此函数在区间(0,1)内为( )
| A.单调递减, | B.有增有减 | C.单调递增, | D.不确定 |
设函数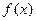 和g(x
和g(x )分别是R上的偶函数和奇函数,则下列结论恒成立的是
)分别是R上的偶函数和奇函数,则下列结论恒成立的是
A.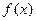 +|g(x)|是偶函数 +|g(x)|是偶函数 | B.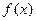 -|g(x)|是奇函数 -|g(x)|是奇函数 |
C.|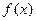 | +g(x)是偶函数 | +g(x)是偶函数 | D.|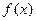 |- g(x)是奇函数 |- g(x)是奇函数 |
设函数f(x)是定义在R上周期为3的奇函数,若f(1)<1,f(2)=,则
| A.a<-1或a>0 | B.-1<a<0 |
| C.a<且a≠-1 | D.-1<a<2 |
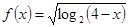 的定义域为( )
的定义域为( )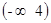 B.
B.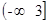 C.
C.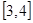 D.
D.