题目内容
若
=(-3,0),
=(
,
),
=(-2,-4),则
=( )
| a |
| b |
| 1 |
| 3 |
| 4 |
| 3 |
| c |
| c |
A、
| ||||||
B、3
| ||||||
C、
| ||||||
D、3
|
分析:把向量
表示为x
+y
的形式,代入坐标运算,使得对应项相等,解除其中的x 和y,就是要求的
和
的系数,得到结论.
| c |
| a |
| b |
| a |
| b |
解答:解:设
=x
+y
,
∴(-2,-4)=x(-3,0)+y(
,
)
∴-2=-3x+
y,-4=
y,
x=
,y=-3
故选C
| c |
| a |
| b |
∴(-2,-4)=x(-3,0)+y(
| 1 |
| 3 |
| 4 |
| 3 |
∴-2=-3x+
| 1 |
| 3 |
| 4 |
| 3 |
x=
| 1 |
| 3 |
故选C
点评:认识向量的代数特性.向量的坐标表示,实现了“形”与“数”的互相转化.以向量为工具,几何问题可以代数化,代数问题可以几何化.

练习册系列答案
相关题目
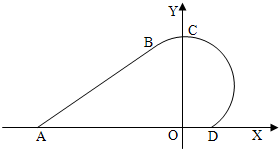 如图,圆弧BCD的圆心P在y轴上,直线AB切圆弧于B,若A(-3,0),
如图,圆弧BCD的圆心P在y轴上,直线AB切圆弧于B,若A(-3,0),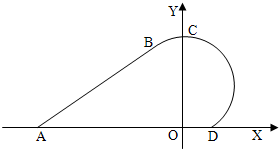 如图,圆弧BCD的圆心P在y轴上,直线AB切圆弧于B,若A(-3,0),
如图,圆弧BCD的圆心P在y轴上,直线AB切圆弧于B,若A(-3,0),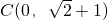 ,D(1,0)
,D(1,0)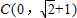 ,D(1,0)
,D(1,0)