题目内容
设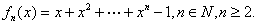
(I)求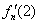 ;[来源:Zxxk.Com]
;[来源:Zxxk.Com]
(II)证明: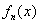 在
在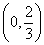 内有且仅有一个零点(记为
内有且仅有一个零点(记为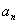 ),且
),且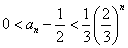 .
.
(I)由题设 ,
,
所以 ①
①
由  ②
②
① ②得
②得
 ,
,
所以 
(II)因为
 ,
,
所以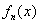 在
在 内至少存在一个零点,
内至少存在一个零点,
又
所以 在
在 内单调递增,
内单调递增,
因此, 在
在 内有且只有一个零点
内有且只有一个零点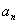 ,
,
由于 ,
,
所以
由此可得
故
所以

练习册系列答案
相关题目
题目内容
设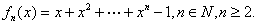
(I)求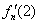 ;[来源:Zxxk.Com]
;[来源:Zxxk.Com]
(II)证明: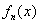 在
在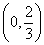 内有且仅有一个零点(记为
内有且仅有一个零点(记为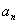 ),且
),且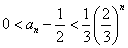 .
.
(I)由题设 ,
,
所以 ①
①
由  ②
②
① ②得
②得
 ,
,
所以 
(II)因为
 ,
,
所以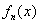 在
在 内至少存在一个零点,
内至少存在一个零点,
又
所以 在
在 内单调递增,
内单调递增,
因此, 在
在 内有且只有一个零点
内有且只有一个零点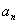 ,
,
由于 ,
,
所以
由此可得
故
所以
