题目内容
9.已知3x+5y+14=0,其中x∈[-3,2],求:|$\frac{y-2}{x+1}$|的最小值.分析 设k=$\frac{y-2}{x+1}$,根据斜率公式求出k的取值范围即可.
解答 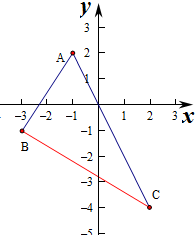 解:设k=$\frac{y-2}{x+1}$,则k的几何意义为线段BC上的点与点A(-1,2)的斜率,
解:设k=$\frac{y-2}{x+1}$,则k的几何意义为线段BC上的点与点A(-1,2)的斜率,
当x=-3时,y=-1,即B(-3,-1),
当x=2时,y=-4,即C(2,-4),
则kAB=$\frac{-1-2}{-3+1}=\frac{-3}{-2}$=$\frac{3}{2}$,kAC=$\frac{-4-2}{2+1}=\frac{-6}{3}$=-2,
即k≥$\frac{3}{2}$或k≤-2,
当k>0时,|k|≥$\frac{3}{2}$,
当k<0时,|k|≥2,
即|$\frac{y-2}{x+1}$|的最小值为$\frac{3}{2}$.
点评 本题主要考查直线斜率的计算,利用数形结合是解决本题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
19.若角α与角β的终边重合,则有( )
| A. | α=π+β | B. | α=-β | C. | α=2kπ-β | D. | α=2kπ+β |