题目内容
已知函数 ,其中
,其中 .
.
(Ⅰ) 求函数 的极小值点;
的极小值点;
(Ⅱ)若曲线 在点
在点 处的切线都与
处的切线都与 轴垂直,问是否存在常数
轴垂直,问是否存在常数 ,使函数
,使函数 在区间
在区间 上存在零点?如果存在,求
上存在零点?如果存在,求 的值:如果不存在,请说明理由.
的值:如果不存在,请说明理由.
请考生在22,23,24三题中任选一题做答,如果多做,则按所做的第一题记分.做答时用2B铅笔在答题卡把所选题目的题号涂黑
【答案】
解:(Ⅰ) 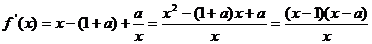
令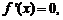 得到
得到 .
.
(1) 当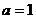 时,
时,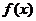 在定义域单调递增,没有极小值点.
在定义域单调递增,没有极小值点.
(2)当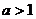 时,当
时,当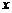 变化时,
变化时,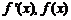 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
极大值 |
|
极小值 |
|
所以 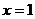 是函数的极大值点.
是函数的极大值点.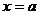 是函数的极小值点.
是函数的极小值点.
(3) 当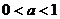 时,
时,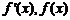 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
极大值 |
|
极小值 |
|
所以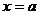 是函数的极大值点.
是函数的极大值点.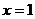 是函数的极小值点.
是函数的极小值点.
综合上述.当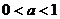 时,
时,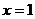 是函数的极小值点. 当
是函数的极小值点. 当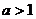 时,
时, 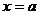 是函数的极小值点.-------6分
是函数的极小值点.-------6分
(Ⅱ)若曲线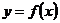 上有两点
上有两点 ,
,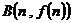 处的切线都与
处的切线都与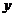 轴垂直,则
轴垂直,则 ,由(Ⅰ)的讨论知,
,由(Ⅰ)的讨论知,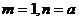 或
或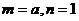 ,
,
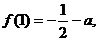 ,
,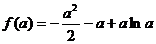 .
.
若函数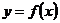 在区间
在区间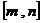 上存在零点,且单调,所以
上存在零点,且单调,所以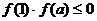 .
.
即 .所以
.所以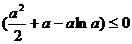 .
.
故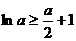 .
.
下面证明此不等式不成立.
令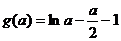 ,则
,则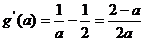 ,
,
于是当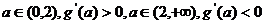 ,所以,
,所以,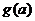 在
在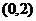 单调递增,在
单调递增,在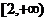 单调递减,所以函数
单调递减,所以函数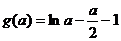 在
在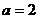 取得最大值
取得最大值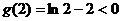 .
.
所以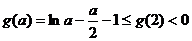 ,所以
,所以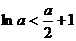 .故不存在满足要求的常数
.故不存在满足要求的常数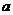 .
.
-------12分

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目






















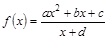 (其中
(其中 是实数常数,
是实数常数, )
) ,函数
,函数 的图像关于点(—1,3)成中心对称,求
的图像关于点(—1,3)成中心对称,求 的值;
的值; ,总有
,总有 ,求
,求 的取值范围;
的取值范围; ,
, ,且对任意
,且对任意 时,不等式
时,不等式 恒成立,求负实数
恒成立,求负实数 的取值范围.
的取值范围.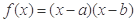 (其中
(其中 )的图象如图(上)所示,则函数
)的图象如图(上)所示,则函数 的图象是( )
的图象是( ) 
