Question

【题目】如图，游客从某旅游景区的景点A处下山至C处有两种路径．一种是从A沿直线步行到C，另一种是先从A沿索道乘缆车到B，然后从B沿直线步行到C．现有甲、乙两位游客从A处下山，甲沿AC匀速步行，速度为50m/min．在甲出发2min后，乙从A乘缆车到B，在B处停留1min后，再从B匀速步行到C．假设缆车匀速直线运动的速度为130m/min，山路AC长为1260m，经测量，cosA= ，cosC=
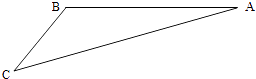
（1）求索道AB的长；
（2）问乙出发多少分钟后，乙在缆车上与甲的距离最短？
（3）为使两位游客在C处互相等待的时间不超过3分钟，乙步行的速度应控制在什么范围内？

Answer 1

【答案】
（1）解：在△ABC中，因为cosA= ，cosC= ，所以sinA= ，sinC= ，

从而sinB=sin[π﹣（A+C）]=sin（A+C）=sinAcosC+cosAsinC= =

由正弦定理 ，得AB= = =1040m．

所以索道AB的长为1040m．

（2）解：假设乙出发t分钟后，甲、乙两游客距离为d，此时，甲行走了（100+50t）m，乙距离A处130t m，所以由余弦定理得

d2=（100+50t）2+（130t）2﹣2×130t×（100+50t）× =200（37t2﹣70t+50）=200[37（t﹣ ）2+ ]，

因0≤t≤ ，即0≤t≤8，故当t= min时，甲、乙两游客距离最短

（3）解：由正弦定理 ，得BC= = =500m，

乙从B出发时，甲已经走了50×（2+8+1）=550m，还需走710m才能到达C．

设乙步行的速度为 v m/min，由题意得﹣3≤ ≤3，解得 ，所以为使两位游客在C处互相等待的时间不超过3分钟，乙步行的速度应控制在[ ]范围内

【解析】（1）根据正弦定理即可确定出AB的长；（2）设乙出发t分钟后，甲、乙两游客距离为d，此时，甲行走了（100+50t）m，乙距离A处130t m，由余弦定理可得；（3）设乙步行的速度为 v m/min，从而求出v的取值范围．