题目内容
【题目】如图，梯形ABCD内接于⊙O，AD∥BC，过点C作⊙O的切线，交BD的延长线于点P，交AD的延长线于点E．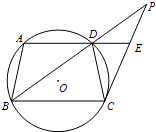 
（1）求证：AB2=DEBC；
（2）若BD=9，AB=6，BC=9，求切线PC的长．
【答案】
（1）解：∵AD∥BC
∴AB=DC，∠EDC=∠BCD，
又PC与⊙O相切，∴∠ECD=∠DBC，
∴△CDE∽△BCD，∴ 
，
∴CD2=DEBC，即AB2=DEBC
（2）解：由（1）知， 
，
∵△PDE∽△PBC，
∴ 
．
又∵PB﹣PD=9，
∴ 
．
∴ 
．
∴ 
【解析】对于（1）求证：AB2=DEBC，根据题目可以判断出梯形为等腰梯形，故AB=CD，然后根据角的相等证△CDE相似于△BCD，根据相似的性质即可得到答案．
对于（2）由BD=9，AB=6，BC=9，求切线PC的长．根据弦切公式可得PC2=PDPB，然后根据相似三角形边成比例的性质求出PD和PB代入即可求得答案．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
