题目内容
已知 ,则方程
,则方程 的实根个数
的实根个数
| A.2 | B.3 | C.4 | D.5 |
A
解析试题分析:因为利用指数函数图像和对数函数图像可知,作出图像函数y=  与y= |
与y= | |,因为底数0<a<1,那么可知其交点个数为2个,因此选A.
|,因为底数0<a<1,那么可知其交点个数为2个,因此选A.
考点:本题主要考查了函数与方程的思想的运用。
点评:解决该试题的关键是分离函数,转换为利用函数y=  与y= |
与y= | |的图像的交点问题来得到实根的个数问题。
|的图像的交点问题来得到实根的个数问题。

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
设函数 ,则满足
,则满足 的x的取值范围是
的x的取值范围是
A. ,2] ,2] | B.[0,2] |
C.[1,+ ] ] | D.[0,+ ] ] |
.计算 ( )
( )
| A.0 | B.1 | C.2 | D.4 |
幂函数的图象过点(2,  ), 则它的单调递增区间是( )
), 则它的单调递增区间是( )
| A.(-∞, 0) | B.[0, +∞) |
| C.(0, +∞) | D.(-∞, +∞) |
函数 ,
,  ,则函数值
,则函数值 的取值范围是( )
的取值范围是( )
A.{ ≤ ≤ ≤5} ≤5} | B. | C.{ } } | D. |
设函数 是定义在R上的奇函数,且
是定义在R上的奇函数,且 ,则
,则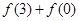 =( )
=( )
| A.3 | B. | C.2 | D. |
计算 的结果为( )
的结果为( )
A. | B. | C. | D. |
 时,函数
时,函数 的值域为
的值域为 , 则实数的取值范围是( )
, 则实数的取值范围是( ) B
B  C
C  D
D 
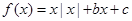 ,给出下列四个命题:
,给出下列四个命题: 时,函数
时,函数 是单调函数
是单调函数 时,方程
时,方程 只有一个实根
只有一个实根 对称
对称