题目内容
下表是A市住宅楼房屋销售价格y和房屋面积x的有关数据:

(I)画出数据对应的散点图;
(II)设线性回归方程为
=bx+a,已计算得b=0.196,
=23.2,计算
及a;
(III)据(II)的结果,估计面积为120m2的房屋销售价格.

(I)画出数据对应的散点图;
(II)设线性回归方程为
| ? |
| y |
. |
| y |
. |
| x |
(III)据(II)的结果,估计面积为120m2的房屋销售价格.
分析:(I)根据表中所给的五对数据,在平面直角坐标系中描出这五个点,得到这组数据的散点图.
(II)根据表中所给的数据,求出横标的平均数,把求得的数据代入求线性回归方程的系数的公式,利用最小二乘法得到结果,写出线性回归方程.
(III)根据第二问求得的线性回归方程,代入所给的x的值,预报出销售价格的估计值,这个数字不是一个准确数值.
(II)根据表中所给的数据,求出横标的平均数,把求得的数据代入求线性回归方程的系数的公式,利用最小二乘法得到结果,写出线性回归方程.
(III)根据第二问求得的线性回归方程,代入所给的x的值,预报出销售价格的估计值,这个数字不是一个准确数值.
解答:解:(I)根据表中所给的数据,写出对应的点的坐标,画出对应的散点图  …(3分)
…(3分)
(II)做出
=
xi=109.
∵
=23.2,
∴样本中心点是(109,23.2)
把样本中心点代入线性回归方程得到
a=
-b
=23.2-109×0.196=1.836.….(7分)
(III)由(II)知,回归直线方程为
=0.196x+1.836.…..(9分)
所以,当x=120m2时,销售价格的估计值为
=0.196×120+1.836=25.356(万元)
所以面积为120m2的房屋销售价格估计为25.356万元.…(12分)
 …(3分)
…(3分)(II)做出
. |
| x |
| 1 |
| 5 |
| 5 |
 |
| i=1 |
∵
. |
| y |
∴样本中心点是(109,23.2)
把样本中心点代入线性回归方程得到
a=
. |
| y |
. |
| x |
(III)由(II)知,回归直线方程为
| ? |
| y |
所以,当x=120m2时,销售价格的估计值为
. |
| y |
所以面积为120m2的房屋销售价格估计为25.356万元.…(12分)
点评:本题考查线性回归分析,考查散点图和估计y的值,本题解题的关键是正确求出横标的平均数,得到样本中心点,在一些题目中正确运算时解题的关键,本题是一个中档题目.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
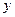 和房屋面积
和房屋面积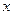 的有关数据:
的有关数据: 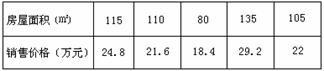
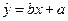 ,已计算得
,已计算得 ,
,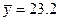 ,计算
,计算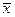 及
及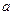 ;
;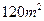 的房屋销售价格.
的房屋销售价格. 和房屋面积
和房屋面积 的有关数据:
的有关数据:

 ,已计算得
,已计算得 ,
, ,计算
,计算 及
及 ;
; 的房屋销售价格.
的房屋销售价格.
 ,已计算得b=0.196,
,已计算得b=0.196, ,计算
,计算 及a;
及a; 下表是A市住宅楼房屋销售价格
下表是A市住宅楼房屋销售价格