题目内容
如图,是一个空间几何体的三视图,则该几何体的外接球的表面积为
分析:由三视图判断出几何体是直三棱锥,且底面是等腰直角三角形,求出对应的高和底面的边长,根据它的外接球是对应直三棱锥的外接球,由外接球的结构特征,求出它的半径,代入表面积公式进行求解.
解答:解:由三视图知该几何体是直三棱锥,且底面是等腰直角三角形,
直三棱锥的高是2,底面的直角边长为
,斜边为2,
则直三棱锥的外接球是对应直三棱柱的外接球,
设几何体外接球的半径为R,因底面是等腰直角三角形,则底面外接圆的半径为1,
∴R2=1+1=2,故外接球的表面积是4πR2=8π,
故答案为:8π.
直三棱锥的高是2,底面的直角边长为
| 2 |
则直三棱锥的外接球是对应直三棱柱的外接球,
设几何体外接球的半径为R,因底面是等腰直角三角形,则底面外接圆的半径为1,
∴R2=1+1=2,故外接球的表面积是4πR2=8π,
故答案为:8π.
点评:本题考查了由三视图求几何体的体积,关键是对几何体正确还原,并根据三视图的长度求出几何体的几何元素的长度,还需要求出外接球的半径,进而求出它的表面积,考查了空间想象能力.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 已知一个空间几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何的体积是
已知一个空间几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何的体积是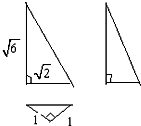 如图是一个空间几何体的三视图,则该几何体外接球的表面积是
如图是一个空间几何体的三视图,则该几何体外接球的表面积是

 B.
B.
 D.
D.
